练习册

  • 练习册
  • 试题
    如图2.若AB∥CD.则可得出 A．∠1＝∠4 B．∠3＝∠5 C．∠4＝∠5 D．∠3＝∠4 【查看更多】

     

    题目列表(包括答案和解析)

    如图，在四边形ABCD中，AB＝CD，E、F分别是BC、AD的中点，连结EF并延长，分别与BA、CD的延长线交于点M、N，则∠BME＝∠CNE(不需证明)．

    (温馨提示：在下图中，连结BD，取BD的中点H，连结HE、HF，根据三角形中位线定理，证明HE＝HF，从而∠1＝∠2，再利用平行线性质，可证得∠BME＝∠CNE．)

    问题一：如图，在四边形ADBC中，AB与CD相交于点O，AB＝CD，E、F分别是BC、AD的中点，连结EF，分别交DC、AB于点M、N，判断△OMN的形状，请直接写出结论．

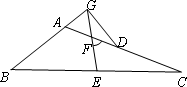
    问题二：如图，在△ABC中，AC＞AB，D点在AC上，AB＝CD，E、F分别是BC、AD的中点，连结EF并延长，与BA的延长线交于点G，若∠EFC＝60°，连结GD，判断△AGD的形状并证明．

    查看答案和解析>>

    如图，在四边形ABCD中，AB＝CD，若要使得四边形ABCD是平行四边形，则还需添加一个条件是________(写出一个即可)．

    查看答案和解析>>

    如图，在等腰梯形ABCD中，AD∥BC，AB＝CD，上底AD＝2，梯形的高也等于2．一动点P从C出发，沿CB方向在线段BC上作匀速运动．

    (1)若三角形ABP的面积S关于运动时间t的函数图象如图所示，则可得BC长为________；

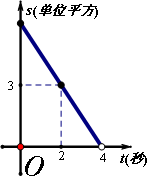
    (2)在(1)的条件下，试求∠B的度数．

    查看答案和解析>>

    如图(a)，AB⊥BD，CD⊥BD，垂足分别为B、D，AD、BC相交于E，过E作EF⊥BD，则可以得到＋＝．

    若将图(a)中的垂直改为斜交，如图(b)，AB∥CD，AD、BC相交于E，过E作EF∥AB交BD于F．试问：

    (1)＋＝还成立吗？请说明理由；

    (2)试找出S△ABD，S△BED，S△BDC间的关系式，并说明理由．

    查看答案和解析>>

    某班同学到野外活动，为测量一池塘两端A、B的距离，设计了几种方案，下面介绍两种：(Ⅰ)如图(1)，先在平地取一个可以直接到达A、B的点C，并分别延长AC到D，BC到E，使DC＝AC，BC＝EC，最后测出DE的距离即为AB的长．(Ⅱ)如图(2)，先过B点作AB的垂线BF，再在BF上取C、D两点，使BC＝CD，接着过点D作BD的垂线DE，交AC的延长线于E，则测出DE的长即为AB的距离．阅读后回答下列问题：

    (1)方案(Ⅰ)是否可行？为什么？

    (2)方案(Ⅱ)是否切实可行？为什么？

    (3)方案(Ⅱ)中作BF⊥AB，ED⊥BF的目的是________；若仅满足∠ABD＝∠BDE≠90°，方案(Ⅱ)是否成立？

    (4)方案(Ⅱ)中，若使BC＝n·CD，能否测得(或求出)AB的长？理由是________，若ED＝m，则AB＝________．

    查看答案和解析>>


    同步练习册答案