
题目列表(包括答案和解析)
本题10分)
操作:小明准备制作棱长为1cm的正方体纸盒,现选用一些废弃的圆形纸片进行如下设计:

纸片利用率=×100%
发现:(1)方案一中的点A、B恰好为该圆一直径的两个端点.你认为小明的这个发现是否正确,请说明理由.
(2)小明通过计算,发现方案一中纸片的利用率仅约为38.2%.请帮忙计算方案二的利用率,并写出求解过程.
探究:(3)小明感觉上面两个方案的利用率均偏低,又进行了新的设计(方案三),请直接写出方案三的利用率.

(本题10分)省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
|
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 |
| 甲 | 10 | 8 | 9 | 8 | 10 | 9 |
| 乙 | 10 | 7 | 10 | 10 | 9 | 8 |
1.(1) 根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环;
2.(2) 分别计算甲、乙六次测试成绩的方差;
3.(3) 根据(1)、(2)计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.
(本题满分10分)某校举行演讲比赛,选出了10名同学担任评委,并事先拟定
从如下4个方案中选择合理的方案来确定每个演讲者的最后得分:
方案1:所有评委所给分的平均数;
方案2:在所有评委所给分中,去掉一个最高分和一个最低分,然后再计算其余
给分的平均数;
方案3:所有评委所给分的中位数;
方案4:所有评委所给分的众数.
为了探究上述方案的合理性,先对某个同学的演讲成绩进行了统计实验,
| 得分 | 3.2 | 7 | 7.8 | 8 | 8.4 | 9.8 |
| 评委人数 | 1人 | 1人 | 1人 | 3人 | 3人 | 1人 |
下面是这个同学的得分统计表:
1.(1)分别按上述4个方案计算这个同学演讲的最后得分;
2.(2)根据(1)中的结果,请用统计的知识说明哪些方案不适合作为这个同学演讲的最后得分.
(本题10分)为了解八年级学生的课外阅读情况,我校语文组从八年级随机抽取了若干名学生,对他们的读书时间进行了调查并将收集的数据绘成了两幅不完整的统计图,请你依据图中提供的信息,解答下列问题:(每组含最小值不含最大值)
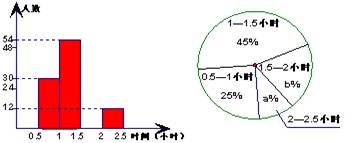
1.⑴从八年级抽取了多少名学生?
2.⑵填空 (直接把答案填到横线上)
①“2—2.5小时”的部分对应的扇形圆心角为_______度;
②课外阅读时间的中位数落在________(填时间段)内.
3.⑶如果八年级共有800名学生,请估算八年级学生课外阅读时间
不少于1.5小时的有多少人?
(本题满分10分)
某商店经销一批小家电,每个小家电的成本为40元。据市场分析,销售单价定为50元时,一个月能售出500件;若销售单价每涨1元,月销售量就减少10件.针对这种小家电的销售情况,请回答以下问题:
(1)当销售单价定为60元时,计算月销售量和月销售利润;
(2)设销售单价定为x元(x>50),月销售利润为y元,求y(用含x的代数式表示);
(3)现该商店要保证每月盈利8750元,同时又要使顾客得到实惠,那么销售单价应定为多少元?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com