若2m＝3，2n＝4，则23m-2n等于（　　）

A．1            B．           C．              D．

在数学学习过程中，通常是利用已有的知识与经验，通过对研究对象进行观察、实验、推理、抽象概括，发现数学规律，揭示研究对象的本质特征。
比如“同底数幂的乘法法则”的学习过程是利用有理数的乘方概念和乘法结合律，由“特殊”到“一般”进行抽象概括的： 2²×2³＝2⁵，2³×2⁴＝2⁷，2²×2⁶＝2⁸，…
2^m×2ⁿ＝2^m+n，…a^m×aⁿ＝a^m+n(m、n都是正整数)。探索问题：
（1）比较下列各组数据的大小：
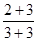①    ， ②   ， ③    ，  ④   ，…。
(2)请你根据上面的材料归纳出a、b、c(a＞b＞0，c＞0)之间的一个数学关系式；并用已学的数学知识说明你发现结论的正确性.
(3)试用(2)中你归纳的数学关系式，解释下面生活中的一个现象：“若m克糖水里含有n克糖，再加入k克糖(仍不饱和)，则糖水更甜了”；

在数学学习过程中，通常是利用已有的知识与经验，通过对研究对象进行观察、实验、推理、抽象概括，发现数学规律，揭示研究对象的本质特征。

比如“同底数幂的乘法法则”的学习过程是利用有理数的乘方概念和乘法结合律，由“特殊”到“一般”进行抽象概括的： 2²×2³＝2⁵，2³×2⁴＝2⁷，2²×2⁶＝2⁸，…

2^m×2ⁿ＝2^m+n，…a^m×aⁿ＝a^m+n(m、n都是正整数)。探索问题：

（1）比较下列各组数据的大小：

①     ，  ②    ，  ③     ，   ④    ，…。

(2)请你根据上面的材料归纳出a、b、c(a＞b＞0，c＞0)之间的一个数学关系式；并用已学的数学知识说明你发现结论的正确性.

(3)试用(2)中你归纳的数学关系式，解释下面生活中的一个现象：“若m克糖水里含有n克糖，再加入k克糖(仍不饱和)，则糖水更甜了”；