根据“角平分线上的点到这个角两边的距离相等”来观察下图：
（1）已知OM是∠AOB的平分线，P是OM上的一点，且PE⊥OA，PF⊥OB．垂足分别为E．F，那么______=______．这是根据“______”可得△POE≌△POF而得到的．
（2）如图，△ABC中，∠C=90°，AC=BC，AD平分∠CAB交BC于D，DE⊥AB，垂足为E，AB=6cm，则△DEB的周长为______cm．

我们都知道，在等腰三角形中．有等边对等角（或等角对等边），那么在不等腰三角形中边与角的大小关系又是怎样的呢？让我们来探究一下．
如图1，在△ABC中，已知AB＞AC，猜想∠B与∠C的大小关系，并证明你的结论；
证明：猜想∠C＞∠B，对于这个猜想我们可以这样来证明：
在AB上截取AD=AC，连接CD，
∵AB＞AC，∴点D必在∠BCA的内部
∴∠BCA＞∠ACD
∵AD=AC，∴∠ACD=∠ADC
又∵∠ADC是△BCD的一个外角，∴∠ADC＞∠B
∴∠BCA＞∠ACD＞∠B 即∠C＞∠B
上面的探究过程是研究图形中不等量关系证明的一种方法，将不等的线段转化为相等的线段，由此解决问题，体现了数学的转化的思想方法．请你仿照类比上述方法，解决下面问题：
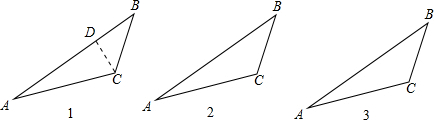
（1）如图2，在△ABC中，已知AC＞BC，猜想∠B与∠A的大小关系，并证明你的结论；
（2）如图3，△ABC中，已知∠C＞∠B，猜想AB与AC大小关系，并证明你的结论；
（3）根据前面得到的结果，请你总结出三角形中边、角不等关系的一般性结论．

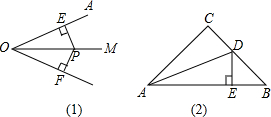
让我们借助平面直角坐标系，一起探索圆的一种奇特的性质．
如图，以平面直角坐标系xOy的原点O为圆心，2个单位长为半径作⊙O，⊙O分别交x轴的负半轴及y轴正半轴于C、D两点，已知A（1，0），B（4，0）．
（1）填空：AC：BC=，AD：BD=；
（2）如果点P是圆上一个动点，那么上述结论是否仍然成立？请以点P在第二象限的情况进行探索．
解：（2）不妨假设点P在第二象限，且没点P坐标为（x，y），
根据勾股定理可得：x²+y²=．（请你继续做下去并在最后对本小题的问题作出回答．）