
题目列表(包括答案和解析)
a、b是两个给定的整数,某同学分别计算当x=-1、1、2、4时代数式ax+b的值,依次得到下列四个结果,已知其中只有三个是正确的,那么错误的一个是
[ ]
(1)分别计算下面甲、乙两个样本的方差,并根据计算结果,判断哪个样本波动较小.
甲:12,13,14,15,10,16,13,11,15,11;
乙:11,16,17,14,13,19,6,8,10,16.
(2)描述一个样本的波动大小,可以采用不止一种方法.我们将样本中各数据与样本平均数的差的绝对值的平均数,叫做这个样本的平均差.样本平均差也是衡量一个样本波动大小的量,样本平均差越大,说明样本的波动越大.例如,样本0、2、4的平均数是2,这个样本的平均差是
试分别计算(1)中甲、乙两个样本的平均差.
从计算结果看,样本的平均差能区分这两个样本的波动大小吗?
研究所对某种新型产品的产销情况进行了研究,为投资商在甲、乙两地生产并销售该产品提供了如下成果:第一年的年产量为x(吨)时,所需的全部费用y(万元)与x满足关系式y=![]() x2+5x+90,投入市场后当年能全部售出,且在甲、乙两地每吨的售价p甲,p乙(万元)均与x满足一次函数关系.(注:年利润=年销售额-全部费用)
x2+5x+90,投入市场后当年能全部售出,且在甲、乙两地每吨的售价p甲,p乙(万元)均与x满足一次函数关系.(注:年利润=年销售额-全部费用)
(1)成果表明,在甲地生产并销售x吨时,p甲=-![]() x+14,请你用含x的代数式表示甲地当年的年销售额,并求年利润w甲(万元)与x之间的函数关系式;
x+14,请你用含x的代数式表示甲地当年的年销售额,并求年利润w甲(万元)与x之间的函数关系式;
(2)成果表明,在乙地生产并销售x吨时,p乙=-![]() x+n(n为常数),且在乙地当年的最大年利润为35万元.试确定n的值;
x+n(n为常数),且在乙地当年的最大年利润为35万元.试确定n的值;
(3)受资金、生产能力等多种因素的影响,某投资商计划第一年生产并销售该产品18吨,根据(1),(2)中的结果,请你通过计算帮他决策,选择在甲地还是乙地产销才能获得较大的年利润?
参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标是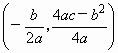 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com