
题目列表(包括答案和解析)
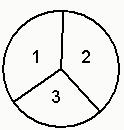 指针所指数字之和为奇数,顾客可获得两次数字之和的9倍的购物券,④其余情况无奖;若顾客不愿转动转盘,可直接获得30元购物券.
指针所指数字之和为奇数,顾客可获得两次数字之和的9倍的购物券,④其余情况无奖;若顾客不愿转动转盘,可直接获得30元购物券. 指针所指数字之和为奇数,顾客可获得两次数字之和的9倍的购物券,④其余情况无奖;若顾客不愿转动转盘,可直接获得30元购物券.
指针所指数字之和为奇数,顾客可获得两次数字之和的9倍的购物券,④其余情况无奖;若顾客不愿转动转盘,可直接获得30元购物券.

若矩形的周长为1,则可求出该矩形面积的最大值.我们可以设矩形的一边长为![]() ,面积为
,面积为![]() ,则
,则![]() 与
与![]() 的函数关系式为:
的函数关系式为: ![]() ﹥0),利用函数的图象或通过配方均可
﹥0),利用函数的图象或通过配方均可
求得该函数的最大值.
提出新问题
若矩形的面积为1,则该矩形的周长有无最大值或最小值?若有,最大(小)值是多少?
分析问题
若设该矩形的一边长为![]() ,周长为
,周长为![]() ,则
,则![]() 与
与![]() 的函数关系式为:
的函数关系式为:![]()
(![]() ﹥0),问题就转化为研究该函数的最大(小)值了.
﹥0),问题就转化为研究该函数的最大(小)值了.
解决问题
借鉴我们已有的研究函数的经验,探索函数![]() (
(![]() ﹥0)的最大(小)值.
﹥0)的最大(小)值.

 (1)实践操作:填写下表,并用描点法画出函数
(1)实践操作:填写下表,并用描点法画出函数![]() (
(![]() ﹥0)的图象:
﹥0)的图象:
(2)观察猜想:观察该函数的图象,猜想当![]() = 时,函数
= 时,函数![]() (
(![]() ﹥0)
﹥0)
有最 值(填“大”或“小”),是 .
(3)推理论证:问题背景中提到,通过配方可求二次函数![]() ﹥0)的最
﹥0)的最
大值,请你尝试通过配方求函数![]() (
(![]() ﹥0)的最大(小)值,以证明你的
﹥0)的最大(小)值,以证明你的
猜想. 〔提示:当![]() >0时,
>0时,![]() 〕
〕
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com