先阅读短文,再回答短文后面的问题.
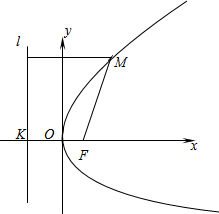
平面内与一个定点F和一条定直线l的距离相等的点的轨迹叫做抛物线,点F叫做抛物线的焦点,直线l叫做抛物线的准线.
下面根据抛物线的定义,我们来求抛物线的方程.
如上图,建立直角坐标系xoy,使x轴经过点F且垂直于直线l,垂足为K,并使原点与线段KF的中点重合.设|KF|=p(p>0),那么焦点F的坐标为(
,0),准线l的方程为x=-
.
设点M(x,y)是抛物线上任意一点,点M到l的距离为d,由抛物线的定义,抛物线就是满足|MF|=d的点M的轨迹.
∵|MF|=
,d=|x+
|∴
=|x+
|
将上式两边平方并化简,得y
2=2px(p>0)①
方程①叫做抛物线的标准方程,它表示的抛物线的焦点在x轴的正半轴上,坐标是(
,0),它的准线方程是x=-
.
一条抛物线,由于它在坐标平面内的位置不同,方程也不同.所以抛物线的标准方程还有其它的几种形式:y
2=-2px,x
2=2py,x
2=-2py.这四种抛物线的标准方程,焦点坐标以及准线方程列表如下:
| 标准方程 |
交点坐标 |
准线方程 |
| y2=2px(p>0) |
(,0) |
x=- |
| y2=-2px(p>0) |
(-,0) |
x= |
| x2=2py(p>0) |
(0,) |
y=- |
| x2=-2py(p>0) |
(0,-) |
y=- |
解答下列问题:
(1)①已知抛物线的标准方程是y
2=8x,则它的焦点坐标是
,准线方程是
②已知抛物线的焦点坐标是F(0,-6),则它的标准方程是
.
(2)点M与点F(4,0)的距离比它到直线l:x+5=0的距离小1,求点M的轨迹方程.
(3)直线
y=x+b经过抛物线y
2=4x的焦点,与抛物线相交于两点A、B,求线段AB的长.

 先阅读短文,再回答短文后面的问题.
先阅读短文,再回答短文后面的问题.