
题目列表(包括答案和解析)
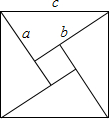 我国古代把直角三角形中较短的直角边称为勾,较长的称为股,斜边称为弦.如图称为“弦图”,最早是由三国时期的数学家赵爽在《周髀算经》中给出的,你能根据“弦图”说明勾股定理的正确性吗?(并写出解答过程)
我国古代把直角三角形中较短的直角边称为勾,较长的称为股,斜边称为弦.如图称为“弦图”,最早是由三国时期的数学家赵爽在《周髀算经》中给出的,你能根据“弦图”说明勾股定理的正确性吗?(并写出解答过程) 我国古代把直角三角形中较短的直角边称为勾,较长的称为股,斜边称为弦.如图称为“弦图”,最早是由三国时期的数学家赵爽在《周髀算经》中给出的,你能根据“弦图”说明勾股定理的正确性吗?(并写出解答过程)
我国古代把直角三角形中较短的直角边称为勾,较长的称为股,斜边称为弦.如图称为“弦图”,最早是由三国时期的数学家赵爽在《周髀算经》中给出的,你能根据“弦图”说明勾股定理的正确性吗?(并写出解答过程)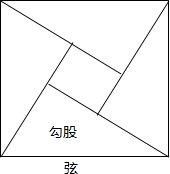 如图:是由四个直角三角形所围成的最著名的赵爽弦图,由弦(c)所围成的正方形面积为12,以勾(a)股(b)之差相乘的中间小正方形面积为1,则(a+b)2的值是( )
如图:是由四个直角三角形所围成的最著名的赵爽弦图,由弦(c)所围成的正方形面积为12,以勾(a)股(b)之差相乘的中间小正方形面积为1,则(a+b)2的值是( )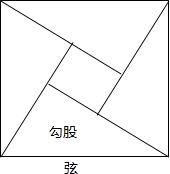 如图:是由四个直角三角形所围成的最著名的赵爽弦图,由弦(c)所围成的正方形面积为12,以勾(a)股(b)之差相乘的中间小正方形面积为1,则(a+b)2的值是
如图:是由四个直角三角形所围成的最著名的赵爽弦图,由弦(c)所围成的正方形面积为12,以勾(a)股(b)之差相乘的中间小正方形面积为1,则(a+b)2的值是| x2+48 |
| x2+48 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com