
题目列表(包括答案和解析)
(本题12分)阅读材料:如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部的线段的长度叫△ABC的“铅垂高”(h).我们可行出生种计算三角形面积的新方示: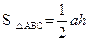 ,即三角形面积等于水平宽与铅垂高乘积的一半.
,即三角形面积等于水平宽与铅垂高乘积的一半.
解答下列问题:
如图2,抛物线顶点C(1,4),交x轴于点A(3,0),交y轴于点B.
(1)求抛物线和直线AB的解析式;
(2)求△ABC的铅垂高CD及S△ABC
(3)设点P是抛物线(在第一象限内)上的一个动点,是否存在一点P,使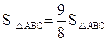 ,
,
若存在,求出P点的坐标;若不存在,请说明理由.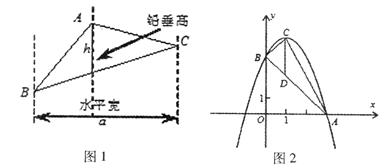
(本题12分)
如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”.如: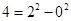 ,
,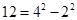 ,
,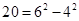 ,因此
,因此 ,
,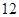 ,
, 这三个数都是神秘数.
这三个数都是神秘数.
(1)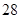 和
和 这两个数是神秘数吗?为什么?
这两个数是神秘数吗?为什么?
(2)设两个连续偶数为 和
和 (其中
(其中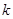 取非负整数),由这两个连续偶数构造的神秘数是
取非负整数),由这两个连续偶数构造的神秘数是 的倍数吗?为什么?
的倍数吗?为什么?
(3)两个连续奇数的平方差(取正数)是神秘数吗?为什么?
(本题12分)
1.(1)学习《测量建筑物的高度》后,小明带着卷尺、标杆,利用太阳光去测量旗杆的高度.参考示意图1,他的测量方案如下:

第一步,测量数据.测出CD=1.6米,CF=1.2米, AE=9米.
第二步,计算.
请你依据小明的测量方案计算出旗杆的高度.
2.(2) 如图2,校园内旗杆周围有护栏,下面有底 座.现在有卷尺、 标杆、平面镜、测角仪等工具,请你选择出必须的工具,设计一个测量方案以求出旗杆顶端到地面的距离.要求:在备用图中画出示意图,说明需要测量的数据.(注意不能到达底部点N对完成测量任务的影响,不需计算)你选择出的必须工具是 ;需要测量的数据是 .

(本题12分)已知两直线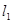 ,
, 分别经过点A(3,0),点B(-1,0),并且当两直线同时相交于y负半轴的点C时,恰好有
分别经过点A(3,0),点B(-1,0),并且当两直线同时相交于y负半轴的点C时,恰好有 ,经过点A、B、C的抛物线的对称轴与直线
,经过点A、B、C的抛物线的对称轴与直线 交于点D,如图所示。
交于点D,如图所示。
(1)求抛物线的函数解析式;
(2)当直线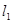 绕点C顺时针旋转一个锐角时,它与抛物线的另一个交点为P(x,y),求四边形APCB面积S关于x的函数解析式,并求S的最大值;
绕点C顺时针旋转一个锐角时,它与抛物线的另一个交点为P(x,y),求四边形APCB面积S关于x的函数解析式,并求S的最大值;
(3)当直线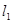 绕点C旋转时,它与抛物线的另一个交点为P,请找出使△PCD为等腰三角形的点P,并求出点P的坐标。
绕点C旋转时,它与抛物线的另一个交点为P,请找出使△PCD为等腰三角形的点P,并求出点P的坐标。
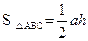 ,即三角形面积等于水平宽与铅垂高乘积的一半.
,即三角形面积等于水平宽与铅垂高乘积的一半.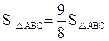 ,
,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com