练习册

  • 练习册
  • 试题
    如图, △ABC中, ∠BAC=90°,AD是△ABC的角平分线, 再作DE∥AC,DF ∥AB.问: (1) 四边形AEDF是矩形吗?请说明理由. (2)四边形AEDF是正方形吗? 请说明理由. 【查看更多】

     

    题目列表(包括答案和解析)

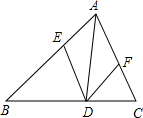    如图，△ABC中，DE∥AC交AB于E，DF∥AB交AC于F，AD是△ABC的角平分线，那么四边形AEDF的形状是
    菱
    菱
    形；在前面的条件下，若△ABC再满足一个条件
    ∠BAC=90°
    ∠BAC=90°
    ，则四边形AEDF是正方形．

    查看答案和解析>>

    如图，在△ABC中，∠ACB是直角，AD、CE分别是∠BAC、∠BCA的平分线，AD、CE相交于点F．
    （1）设∠ABC=m°（0＜m＜90），试用m的代数式表示∠AFE的度数；
    （2）请你给△ABC再添加一个条件，使FE与FD的长度相等，并予以证明；
    （3）在（2）中，你认为“∠ACB是直角”的条件是否可以略去？直接判断，不必说明理由.

    查看答案和解析>>

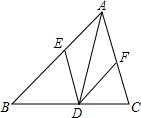    如图△ABC中，DE∥AC交AB于E，DF∥AB交AC于F，
    （1）如果AD是△ABC的角平分线，那么四边形AEDF是
    菱形
    菱形
    形．请证明你的结论．
    （2）在（1）的条件下，给△ABC再添加一个条件：
    ∠BAC=90°（答案不唯一）
    ∠BAC=90°（答案不唯一）
    ，则四边形AEDF是正方形．（只填空，不要证明）

    查看答案和解析>>

    阅读下面材料：
    小炎遇到这样一个问题：如图1，点E、F分别在正方形ABCD的边BC，CD上，∠EAF=45°，连结EF，则EF=BE+DF，试说明理由．
    小炎是这样思考的：要想解决这个问题，首先应想办法将这些分散的线段相对集中．她先后尝试了翻折、旋转、平移的方法，最后发现线段AB，AD是共点并且相等的，于是找到解决问题的方法．她的方法是将△ABE绕着点A逆时针旋转90°得到△ADG，再利用全等的知识解决了这个问题（如图2）．
    参考小炎同学思考问题的方法，解决下列问题：
    （1）如图3，四边形ABCD中，AB=AD，∠BAD=90°点E，F分别在边BC，CD上，∠EAF=45°．若∠B，∠D都不是直角，则当∠B与∠D满足_       关系时，仍有EF=BE+DF；
    （2）如图4，在△ABC中，∠BAC=90°，AB=AC，点D、E均在边BC上，且∠DAE=45°，若BD=1， EC=2，求DE的长．

    查看答案和解析>>


    同步练习册答案