图1是一个长为2m、宽为2n的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图2的形状拼成一个正方形．

（1）你认为图2中的阴影部分的正方形的边长等于______？
（2）请用两种不同的方法求图2中阴影部分的面积．
①______；
②______．
（3）观察图2你能写出下列三个代数式之间的等量关系吗？
（m+n）²，（m-n）²，mn______．
（4）运用你所得到的公式，计算若mn=-2，m-n=4，求（m+n）²的值．
（5）用完全平方公式和非负数的性质求代数式x²+2x+y²-4y+7的最小值．

数学家高斯在读小学二年级时老师出了这样一道计算题：

1+2+3+4+…+100=?

高斯很快得出了答案，他的计算方法是：

1+2+3+…+100=(1+100)+(2+99)+(3+98)+…+(50+51)=50×(1+100)=5050．

(1)请你应用上述方法求S=1+3+5+…+(2n-1)的计算公式；

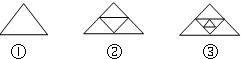
(2)如图，第二个图形是由第一个图形中的三角形连接三边中点而得到的，第三个图形是第二个图形中间一个三角形连结三边中点而得到的，依此类推……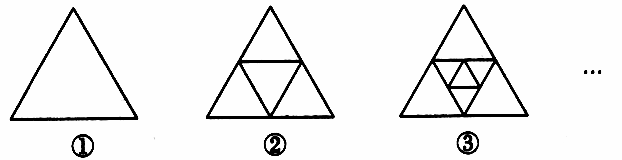

分别写出第二个图形、第三个图形和第四个图形的三角形的个数，由此推测出第n个图形中三角形的个数，并求出第一个图形到第n个图形的三角形个数之和S．