如果一条抛物线y=ax²+bx+c（a≠0）与x轴有两个交点，那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”，[a，b，c]称为“抛物线三角形系数”．
（1）若抛物线三角形系数为[-1，b，0]的“抛物线三角形”是等腰直角三角形，求b的值；
（2）若△OAB是“抛物线三角形”，其中点B为顶点，抛物线三角形系数为[-2，2m，0]，其中m＞0；且四边形ABCD是以原点O为对称中心的矩形，求出过O、C、D三个点的抛物线的表达式．

22、在复习“四边形”时，刘老师出了这样一道题：
如图1，已知四边形ABCD、BEFG都是矩形，点G、H分别在AB、CD上，点B、C、E在同一条直线上．

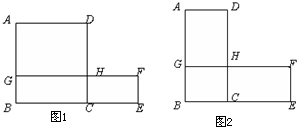
（1）当S_矩形AGHD=S_矩形CEFH时，试画一条直线将整个图形面积2等分．（不写画法）
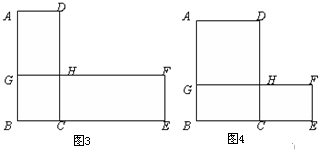
（2）①当S_矩形AGHD＜S_矩形CEFH时，如图3；②当S_矩形AGHD＞S_矩形CEFH时，如图4．画一条直线将整个图形面积2等分，在（1）的基础上，应该如何画图呢？（不写画法，保留作图痕迹或简要的文字说明）
（3）小娟和小宇两位同学的画法是图5和图6：刘老师看过之后说这两个图形实质上体现的是一种画法，请你用简要的文字说明两个图形画法的共同点：．