
题目列表(包括答案和解析)
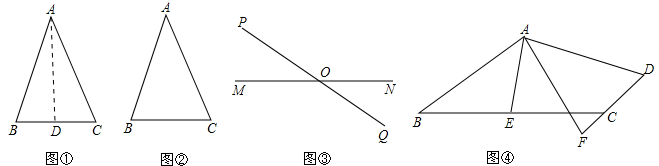
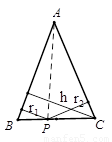
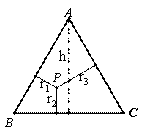
阅读材料:如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两 腰的距离分别为 ,腰上的高为h,连结AP,则
,腰上的高为h,连结AP,则 ,即:
,即: ,
, (1)理解与应用
(1)理解与应用
如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在 三角形内任一点”,即:已知边长为2的等边△ABC内任意一点P到各边的距离分别为 ,
, ,
, ,试证明:
,试证明: .
.

(2)类比与推理
边长为2的正方形内任意一点到各边的距离的和等于 ;
(3)拓展与延伸
若边长为2的正n边形A1A2…An内部任意一点P到各边的距离为 ,请问
,请问 是否为定值(用含n的式子表示),如果是,请合理猜测出这个定值。
是否为定值(用含n的式子表示),如果是,请合理猜测出这个定值。
阅读材料:如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两 腰的距离分别为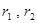 ,腰上的高为h,连结AP,则
,腰上的高为h,连结AP,则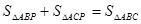 ,即:
,即: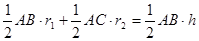 ,
,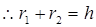 (1)理解与应用
(1)理解与应用
如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在 三角形内任一点”,即:已知边长为2的等边△ABC内任意一点P到各边的距离分别为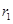 ,
,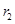 ,
,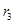 ,试证明:
,试证明: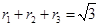 .
.
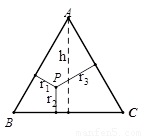
(2)类比与推理
边长为2的正方形内任意一点到各边的距离的和等于 ;
(3)拓展与延伸
若边长为2的正n边形A1A2…An内部任意一点P到各边的距离为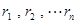 ,请问
,请问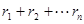 是否为定值(用含n的式子表示),如果是,请合理猜测出这个定值。
是否为定值(用含n的式子表示),如果是,请合理猜测出这个定值。
阅读材料:如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为![]() ,腰上的高为h,连结AP,则
,腰上的高为h,连结AP,则![]() ,即:
,即:![]() ,
,![]()
(1)理解与应用 如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在三角形内任一点”,即:已知边长为2的等边△ABC内任意一点P到各边的距离分别为![]() ,
,![]() ,
,![]() ,试证明:
,试证明:![]() .
.
(2)类比与推理 边长为2的正方形内任意一点到各边的距离的和等于 ;
(3)拓展与延伸 若边长为2的正n边形A1A2…An内部任意一点P到各边的距离为![]() ,请问
,请问![]() 是否为定值(用含n的式子表示),如果是,请合理猜测出这个定值。
是否为定值(用含n的式子表示),如果是,请合理猜测出这个定值。

 23、(1)如图1,在△ABC中,绕点C旋转180°后,得到△CA′B′请先画出变换后的图形,写出下列结论正确的序号是
23、(1)如图1,在△ABC中,绕点C旋转180°后,得到△CA′B′请先画出变换后的图形,写出下列结论正确的序号是湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com