
题目列表(包括答案和解析)
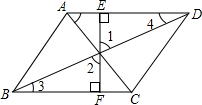 下面是小明作业中对一道题的解答以及老师的批阅
下面是小明作业中对一道题的解答以及老师的批阅
 ∠BAF,∠3=∠4=
∠BAF,∠3=∠4=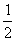 ∠ABE,
∠ABE,  (∠BAF+∠ABE)=90。
(∠BAF+∠ABE)=90。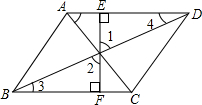 下面是小明作业中对一道题的解答以及老师的批阅
下面是小明作业中对一道题的解答以及老师的批阅 如图,平行四边形ABCD中,AE、CF分别是∠BAD和∠BCD的角平分线,根据现有的图形,请你添加一个条件,使四边形AECF为菱形,并说明理由.
如图,平行四边形ABCD中,AE、CF分别是∠BAD和∠BCD的角平分线,根据现有的图形,请你添加一个条件,使四边形AECF为菱形,并说明理由.(本题10分)如图,在四边形ABCD中,AB=2,CD=1,∠A=61°,
∠ADC=∠B=90°,利用解直角三角形知识求这个四边形ABCD的面积。
(结果精确到0.1。下列数据供参考:
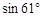 ≈0.87,
≈0.87,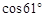 ≈0.48,
≈0.48,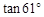 ≈1.80;
≈1.80;
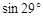 ≈0.48,
≈0.48, ≈0.87,
≈0.87,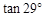 ≈0.55)
≈0.55)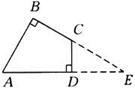
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com