实际问题：某学校共有18个教学班，每班的学生数都是40人．为了解学生课余时间上网情况，学校打算做一次抽样调查，如果要确保全校抽取出来的学生中至少有10人在同一班级，那么全校最少需抽取多少名学生？

建立模型：为解决上面的“实际问题”，我们先建立并研究下面从口袋中摸球的数学模型：

在不透明的口袋中装有红、黄、白三种颜色的小球各20个(除颜色外完全相同)，现要确保从口袋中随机摸出的小球至少有10个是同色的，则最少需摸出多少个小球？

为了找到解决问题的办法，我们可把上述问题简单化：

(1)我们首先考虑最简单的情况：即要确保从口袋中摸出的小球至少有2个是同色的，则最少需摸出多少个小球？

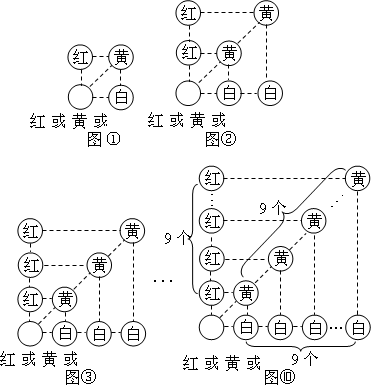
假若从袋中随机摸出3个小球，它们的颜色可能会出现多种情况，其中最不利的情况就是它们的颜色各不相同，那么只需再从袋中摸出1个小球就可确保至少有2个小球同色，即最少需摸出小球的个数是：1＋3＝4(如图①)；

(2)若要确保从口袋中摸出的小球至少有3个是同色的呢？

我们只需在(1)的基础上，再从袋中摸出3个小球，就可确保至少有3个小球同色，即最少需摸出小球的个数是：1＋3×2＝7(如图②)

(3)若要确保从口袋中摸出的小球至少有4个是同色的呢？

我们只需在(2)的基础上，再从袋中摸出3个小球，就可确保至少有4个小球同色，即最少需摸出小球的个数是：1＋3×3＝10(如图③)：

……

(10)若要确保从口袋中摸出的小球至少有10个是同色的呢？

我们只需在(9)的基础上，再从袋中摸出3个小球，就可确保至少有10个小球同色，即最少需摸出小球的个数是：1＋3×(10－1)＝28(如图⑩)

模型拓展一：在不透明的口袋中装有红、黄、白、蓝、绿五种颜色的小球各20个(除颜色外完全相同)，现从袋中随机摸球：

(1)若要确保摸出的小球至少有2个同色，则最少需摸出小球的个数是________；

(2)若要确保摸出的小球至少有10个同色，则最少需摸出小球的个数是________；

(3)若要确保摸出的小球至少有n个同色(n＜20)，则最少需摸出小球的个数是________．

模型拓展二：在不透明口袋中装有m种颜色的小球各20个(除颜色外完全相同)，现从袋中随机摸球：

(1)若要确保摸出的小球至少有2个同色，则最少需摸出小球的个数是________．

(2)若要确保摸出的小球至少有n个同色(n＜20)，则最少需摸出小球的个数是________．

问题解决：(1)请把本题中的“实际问题”转化为一个从口袋中摸球的数学模型；

(2)根据(1)中建立的数学模型，求出全校最少需抽取多少名学生．

已知一次函数y＝＋m(0＜m≤1)的图象为直线l，直线l绕原点O旋转180°后得直线，△ABC三个顶点的坐标分别为A(－，－1)、B(，－1)、C(0，2)．

(1)直线AC的解析式为________，直线的解析式为________(可以含m)；

(2)如图，l、分别与△ABC的两边交于E、F、G、H，当m在其范围内变化时，判断四边形EFGH中有哪些量不随m的变化而变化？并简要说明理由；

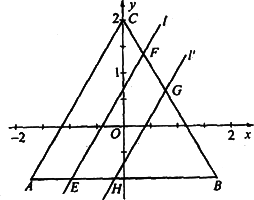
(3)将(2)中四边形EFGH的面积记为S，试求m与S的关系式，并求S的变化范围；

(4)若m＝1，当△ABC分别沿直线y＝x与y＝x平移时，判断△ABC介于直线l，之间部分的面积是否改变？若不变请指出来．若改变请写出面积变化的范围．(不必说明理由)