
题目列表(包括答案和解析)
我们约定,若一个三角形(记为△A1)是由另一个三角形(记为△A)通过一次平移,或绕其任一边的中点旋转180°得到的,则称△A1是由△A复制的.以下的操作中每一个三角形只可以复制一次,复制过程可以一直进行下去.如图1,由△A复制出△A1,又由△A1复制出△A2,再由△A2复制出△A3,形成了一个大三角形,记作△B.以下各题中的复制均是由△A开始的,通过复制形成的多边形中的任意相邻两个小三角形(指与△A全等的三角形)之间既无缝隙也无重叠.
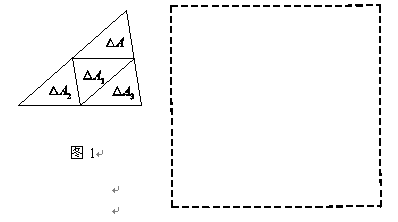
1.(1)图1中标出的是一种可能的复制结果,小明发现△A∽△B,其相似比为_________.在图1的基础上继续复制下去得到△C,若△C的一条边上恰有11个小三角形(指有一条边在该边上的小三角形),则△C中含有______个小三角形;
2.(2)若△A是正三角形,你认为通过复制能形成的正多边形是________;
3. (3)请你用两次旋转和一次平移复制形成一个四边形,在图2的方框内画出草图,并仿照图1作出标记.


 次旋转和一次平移复制形成一个四
次旋转和一次平移复制形成一个四 边形,在图2的方框内画出草图,并仿照图1作出标记.
边形,在图2的方框内画出草图,并仿照图1作出标记.我们约定,若一个三角形(记为△A1)是由另一个三角形(记为△A)通过一次平移,或绕其任一边的中点旋转180°得到的,则称△A1是由△A复制的.以下的操作中每一个三角形只可以复制一次,复制过程可以一直进行下去.如图1,由△A复制出△A1,又由△A1复制出△A2,再由△A2复制出△A3,形成了一个大三角形,记作△B.以下各题中的复制均是由△A开始的,通过复制形成的多边形中的任意相邻两个小三角形(指与△A全等的三角形)之间既无缝隙也无重叠.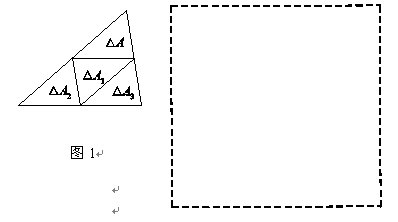
【小题1】(1)图1中标出的是一种可能的复制结果,小明发现△A∽△B,其相似比为_________.在图1的基础上继续复制下去得到△C,若△C的一条边上恰有11个小三角形(指有一条边在该边上的小三角形),则△C中含有______个小三角形;
【小题2】(2)若△A是正三角形,你认为通过复制能形成的正多边形是________;
【小题3】 (3)请你用两
 次旋转和一次平移复制形成一个四
次旋转和一次平移复制形成一个四 边形,在图2的方框内画出草图,并仿照图1作出标记.
边形,在图2的方框内画出草图,并仿照图1作出标记.
我们约定,若一个三角形(记为△A1)是由另一个三角形(记为△A)通过一次平移,或绕其任一边的中点旋转180°得到的,则称△A1是由△A复制的.以下的操作中每一个三角形只可以复制一次,复制过程可以一直进行下去.如图1,由△A复制出△A1,又由△A1复制出△A2,再由△A2复制出△A3,形成了一个大三角形,记作△B.以下各题中的复制均是由△A开始的,通过复制形成的多边形中的任意相邻两个小三角形(指与△A全等的三角形)之间既无缝隙也无重叠.

1.(1)图1中标出的是一种可能的复制结果,小明发现△A∽△B,其相似比为_________.在图1的基础上继续复制下去得到△C,若△C的一条边上恰有11个小三角形(指有一条边在该边上的小三角形),则△C中含有______个小三角形;
2.(2)若△A是正三角形,你认为通过复制能形成的正多边形是________;
3. (3)请你用两次旋转和一次平移复制形成一个四边形,在图2的方框内画出草图,并仿照图1作出标记.
现在初中课本里所学习的概率计算问题只有以下类型:
第一类是可以列举有限个等可能发生的结果的概率计算问题(一步试验直接列举,两步以上的试验可以借助树状图或表格列举),比如掷一枚均匀硬币的试验;
第二类是用试验或者模拟试验的数据计算频率,并用频率估计概率的概率计算问题,比如掷图钉的试验;
解决概率计算问题,可以直接利用模型,也可以转化后再利用模型;
请解决以下问题
(1)如图,类似课本的一个寻宝游戏,若宝物随机藏在某一块砖下(图中每一块砖除颜色外完全相同),则宝物藏在阴影砖下的概率是多少?
(2)在1~9中随机选取3个整数,若以这3个整数为边长构成三角形的情况如下表:
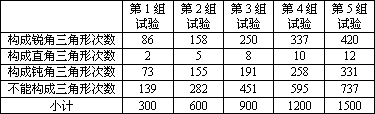
请你根据表中数据,估计构成钝角三角形的概率是多少?(精确到百分位)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com