
题目列表(包括答案和解析)
在等边△ABC中,点D为AC上一点,连结BD,直线l与AB,BD,BC分别相交于点E,P,F,且∠BPF=60°.
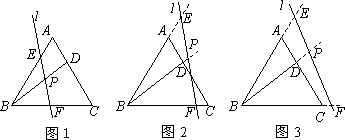
(1)如图1,写出图中所有与△BPF相似的三角形,并选择其中一对给予证明;
(2)若直线l向右平移到图2、图3的位置时(其它条件不变),(1)中的结论是否仍然成立?若成立,请写出来(不证明),若不成立,请说明理由;
(3)探究:如图1,当BD满足什么条件时(其它条件不变),![]() ?请写出探究结果,并说明理由.
?请写出探究结果,并说明理由.
(说明:结论中不得含有未标识的字母)
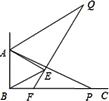
如图,已知∠ABC=90°,△ABE是等边三角形,点P为射线BC上任意一点(点P与点B不重合),连接AP,将线段AP绕点A逆时针旋转60°得到线段AQ,连接QE并延长交射线BC于点F.在下列结论中:①∠QFC=60°;②△AEQ≌△ABP;③BF=EF;④若线段AB=2![]() ,设BP=x,点Q到射线BC的距离为y,则y=
,设BP=x,点Q到射线BC的距离为y,则y=![]() x+
x+![]() (x>0).其中一定正确的结论个数有
(x>0).其中一定正确的结论个数有
A.1个
B.2个
C.3个
D.4个
在课外小组活动时,小伟拿来一道题(原问题)和小熊、小强交流.
原问题:如图1,已知△ABC,∠ACB=90° , ∠ABC=45°,分别以AB、BC为边向外作△ABD与△BCE, 且DA=DB, EB=EC,∠ADB=∠BEC=90°,连接DE交AB于点F. 探究线段DF与EF的数量关系.小伟同学的思路是:过点D作DG⊥AB于G,构造全等三角形,通过推理使问题得解.小熊同学说:我做过一道类似的题目,不同的是∠ABC=30°,∠ADB=∠BEC=60°.小强同学经过合情推理,提出一个猜想,我们可以把问题推广到一般情况.请你参考小慧同学的思路,探究并解决这三位同学提出的问题:
1.写出原问题中DF与EF的数量关系
2.如图2,若∠ABC=30°,∠ADB=∠BEC=60°,原问题中的其他条件不变,你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明;
3.如图3,若∠ADB=∠BEC=2∠ABC,原问题中的其他条件不变,你在(1)中
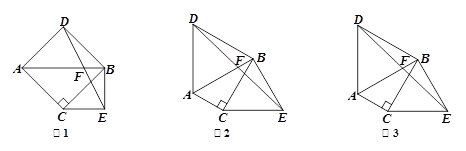
得到的结论是否发生变化?请写出你的猜想并加以证明
在课外小组活动时,小伟拿来一道题(原问题)和小熊、小强交流.
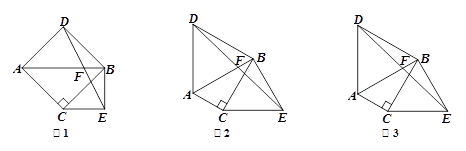
原问题:如图1,已知△ABC, ∠ACB=90°, ∠ABC=45°,分别以AB、BC为边向外作△ABD与△BCE, 且DA=DB, EB=EC,∠ADB=∠BEC=90°,连接DE交AB于点F. 探究线段DF与EF的数量关系.小伟同学的思路是:过点D作DG⊥AB于G,构造全等三角形,通过推理使问题得解.小熊同学说:我做过一道类似的题目,不同的是∠ABC=30°,∠ADB=∠BEC=60°.小强同学经过合情推理,提出一个猜想,我们可以把问题推广到一般情况.请你参考小慧同学的思路,探究并解决这三位同学提出的问题:
【小题1】写出原问题中DF与EF的数量关系
【小题2】如图2,若∠ABC=30°,∠ADB=∠BEC=60°,原问题中的其他条件不变,你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明;
【小题3】如图3,若∠ADB=∠BEC=2∠ABC,原问题中的其他条件不变,你在(1)中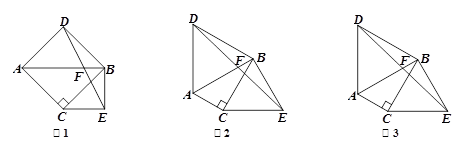
得到的结论是否发生变化?请写出你的猜想并加以证明
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com