在△ABC中，AC＝BC，∠C＝90°，将一块三角板的直角顶点放在斜边AB的中点P处，将三角板绕P点旋转，三角板的两条直角边分别交AC、CB于D、E两点，如图(1)、(2)所示．

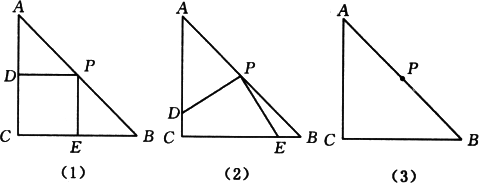
(1)问PD与PE有何大小关系？并以图(2)为例加以说明；

(2)在旋转过程中，还会存在与图(1)、(2)不同的情形吗？若存在，请在图(3)中画出，并说明(1)中PD与PE的大小关系在图(3)中是否还成立？

在△ABC中，AB＝AC＝2，∠A＝90°，取一块含45°角的直角三角尺，将直角顶点放在斜边BC边的中点O处(如图1)，绕O点顺时针方向旋转，使90°角的两边与Rr△ABC的两边AB，AC分别相交于点E，F(如图2)．设BE＝x，CF＝y．

(1)探究：在图2中，线段AE与CF之间有怎样的大小关系？试证明你的结论；

(2)若将直角三角尺45°角的顶点放在斜边BC边的中点O处(如图3)，绕O点顺时针方向旋转，其他条件不变．

①试写出y与x的函数解析式，以及x的取值范围；

②将三角尺绕O点旋转(如图4)的过程中，△OEF是否能成为等腰三角形？若能，直接写出△OEF为等腰三角形时x的值；若不能，请说明理由．

有一副直角三角板，在三角板ABC中，∠BAC＝90°，AB＝AC＝6，在三角板DEF中，∠FDE＝90°，DF＝4，DE＝．将这副直角三角板按如图(1)所示位置摆放，点B与点F重合，直角边BA与FD在同一条直线上．现固定三角板ABC，将三角板DEF沿射线BA方向平行移动，当点F运动到点A时停止运动．

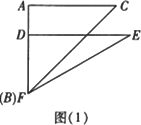
(1)如图(2)，当三角板DEF运动到点D与点A重合时，设EF与BC交于点M，则∠EMC＝________度；

(2)如图(3)，在三角板DEF运动过程中，当EF经过点C时，求FC的长；

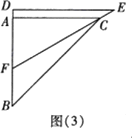
(3)在三角板DEF运动过程中，设BF＝x，两块三角板重叠部分面积为y，求y与x的函数解析式，并求出对应的x取值范围．

我们做如下的规定：如果一个三角形在运动变化时保持形状和大小不变，则把这样的三角形称为三角形板．

把两块边长为4的等边三角形板ABC和DEF叠放在一起，使三角形板DEF的顶点D与三角形板ABC的AC边中点O重合，把三角形板ABC固定不动，让三角形板DEF绕点O旋转，设射线DE与射线AB相交于点M，射线DF与线段BC相交于点N．

(1)如图1，当射线DF经过点B，即点Q与点B重合时，易证△ADM∽△CND．此时，AM·CN＝________．

(2)将三角形板DEF由图1所示的位置绕点O沿逆时针方向旋转，设旋转角为α．其中0°＜α＜90°，问AM·CN的值是否改变？说明你的理由．

(3)在(2)的条件下，设AM＝x，两块三角形板重叠面积为y，求y与x的函数关系式．(图2，图3供解题用)