
题目列表(包括答案和解析)
(![]() )
)![]() +1=2,s1=
+1=2,s1=![]() ;
;
(![]() )
)![]() +1=3,s2=
+1=3,s2=![]() ;
;
(![]() )
)![]() +1=4,s3=
+1=4,s3=![]()

(1)请用含有n(n是正整数)的等式表示上述变化规律;
(2)推算出OA10的长;
(3)求出s12+S22+S32+…+S102的值.
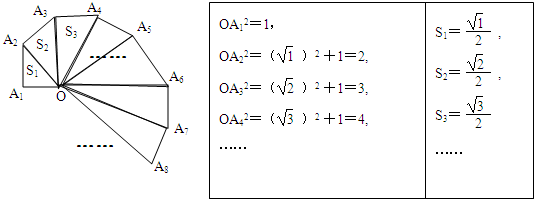
 细心观察图形,认真分析各式,然后解答问题;
细心观察图形,认真分析各式,然后解答问题;| 12+12 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2+12 |
| 3 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| 3+12 |
| 4 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
 细心观察图形,认真分析各式,然后解答问题:
细心观察图形,认真分析各式,然后解答问题:| 1 |
| 2 |
| 2 |
| ||
| 2 |
| 3 |
| ||
| 2 |
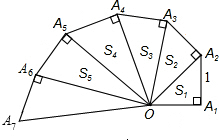 细心观察图形,认真分析各式,然后回答问题:
细心观察图形,认真分析各式,然后回答问题:| 1 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| 3 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 10 |
| 10 |
| 55 |
| 4 |
| 55 |
| 4 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com