
题目列表(包括答案和解析)
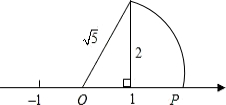 “数轴上的点并不都表示有理数,如图中数轴上的点P所表示的数是
“数轴上的点并不都表示有理数,如图中数轴上的点P所表示的数是| 5 |
| A、代入法 |
| B、换元法 |
| C、数形结合的思想方法 |
| D、分类讨论的思想方法 |
| 方 程 | 换元法得 新方程 | 解 新 方 程 | 检 验 | 求原方程 的解 |
①2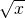 -3=0 -3=0 | 设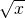 =t =t则2t-3=0 | t=  | t=  >0 >0 | ∵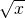 = = ∴x=  |
②x+2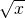 -3=0 -3=0 | ||||
③x+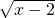 -4=0 -4=0 |
数轴上的点并不都表示有理数,如图以数轴的单位长度为边作正方形,以数轴上的原点O为圆心,正方形的对角线的长为半径作弧与数轴交于一点A,则点A表示的数为 这种说明问题的方式体现的数学思想方法叫做( )
A.代入法 B.换元法 C.数形结合 D.分类讨论

请你模仿上面的例子在下面的数轴上找出表示![]() 的点:(本小题5分 )
的点:(本小题5分 )
 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com