
题目列表(包括答案和解析)
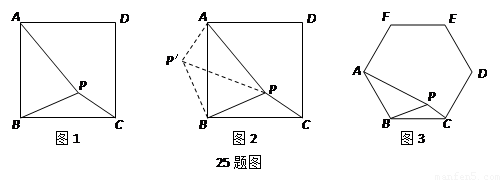
【问题】如图17-1,在正方形ABCD内有一点P,PA=![]() ,PB=
,PB=![]() ,PC=1,求∠BPC的度数.
,PC=1,求∠BPC的度数.
分析根据已知条件比较分散的特点,我们可以通过旋转变换将分散的已知条件集中在一起,于是将△BPC绕点B逆时针旋转90°,得到了△BP′A(如图17-2),然后连结PP′.
解决问题请你通过计算求出图17-2中∠BPC的度数;
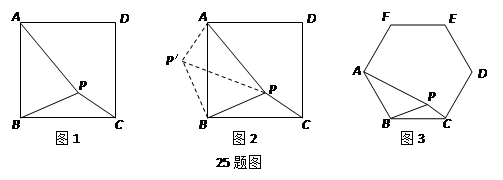
类比研究 如图17-3,若在正六边形ABCDEF内有一点P,且PA=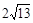 ,PB=4,PC=2.
,PB=4,PC=2.
(1)∠BPC的度数为 ; (2)直接写出正六边形ABCDEF的边长为 .
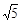 ,PB=
,PB=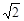 ,PC=1,求∠BPC的度数.
,PC=1,求∠BPC的度数.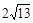 ,PB=4,PC=2.
,PB=4,PC=2.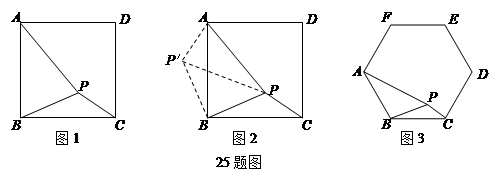
【问题】如图17-1,在正方形ABCD内有一点P,PA=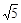 ,PB=
,PB=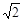 ,PC=1,求∠BPC的度数.
,PC=1,求∠BPC的度数.
分析根据已知条件比较分散的特点,我们可以通过旋转变换将分散的已知条件集中在一起,于是将△BPC绕点B逆时针旋转90°,得到了△BP′A(如图17-2),然后连结PP′.
解决问题请你通过计算求出图17-2中∠BPC的度数;
类比研究 如图17-3,若在正六边形ABCDEF内有一点P,且PA=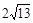 ,PB=4,PC=2.
,PB=4,PC=2.
(1)∠BPC的度数为 ; (2)直接写出正六边形ABCDEF的边长为 .
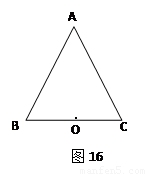
已知点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC
1.如图16,若点O在BC上,求证AB=AC。
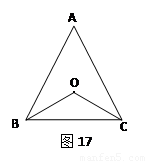
2.如图17,若点O在△ABC内部,求证AB=AC。
3.猜想,若O点在△ABC的外部,AB=AC成立吗?
如图17-1-9所示,已知直线y1=x+m与x轴、y轴分别交于点A、B,与双曲线y2=![]() (k<0)分别交于
(k<0)分别交于![]() 点C、D,且C点坐标为(-1,2).
点C、D,且C点坐标为(-1,2).
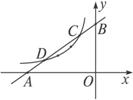
图17-1-9
(1)分别求直线AB与双曲线的解析式;
(2)求出点D的坐标;
(![]() 3)利用图象直接写出当x在什么范围内时,y1>y2.
3)利用图象直接写出当x在什么范围内时,y1>y2.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com