
题目列表(包括答案和解析)
 25、某养殖专业户计划利用房屋的一面墙修造如图所示的长方体水池,培育不同品种的鱼苗.他已准备可以修高为3m.长30m的水池墙的材料,图中EF与房屋的墙壁互相垂直,设AD的长为xm.(不考虑水池墙的厚度)
25、某养殖专业户计划利用房屋的一面墙修造如图所示的长方体水池,培育不同品种的鱼苗.他已准备可以修高为3m.长30m的水池墙的材料,图中EF与房屋的墙壁互相垂直,设AD的长为xm.(不考虑水池墙的厚度)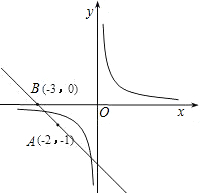 如图,直线y=kx+b经过A(-2,-1)和B(-3,0)两点,利用函数图象判断不等式
如图,直线y=kx+b经过A(-2,-1)和B(-3,0)两点,利用函数图象判断不等式| 1 |
| x |
A、x<
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、x<
|
| 6x2 | 1-x1 |
 的收益z(元)会相应降低,且z与x之间也大致满足z=-3x+3000
的收益z(元)会相应降低,且z与x之间也大致满足z=-3x+3000湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com