
题目列表(包括答案和解析)
| a |
| b |
| c |
| d |
| a |
| c |
| b |
| d |
| a+b |
| b |
| c+d |
| d |
| a+b |
| a-b |
| c+d |
| c-d |
| a |
| b |
| c |
| d |
| a |
| c |
| b |
| d |
| a+b |
| b |
| c+d |
| d |
| a+b |
| a-b |
| c+d |
| c-d |
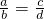 ,根据分式的基本性质、等式的基本性质及运算法则,探究下面各组中的两个分式之间有什么关系?然后选择其中一组进行具体说明.
,根据分式的基本性质、等式的基本性质及运算法则,探究下面各组中的两个分式之间有什么关系?然后选择其中一组进行具体说明.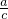 和
和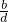 ; (2)
; (2)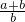 和
和 ; (3)
; (3) 和
和 (a≠b,c≠d).
(a≠b,c≠d).
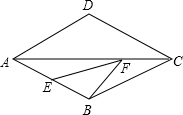 如图所示,在边长为2的菱形ABCD中,∠DAB=60°,点E为AB中点,点F是AC上一动点,则EF+BF的最小值为
如图所示,在边长为2的菱形ABCD中,∠DAB=60°,点E为AB中点,点F是AC上一动点,则EF+BF的最小值为湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com