已知平面直角坐标系上有6个点:A(3,3),B(1,1),C(9,1),D(5,3).E(-1,-9),F(-2,-
)
下面有2个小题,
(1)请将上述的6个点按下列的要求分成两类,并写出同类点具有而另一类点不具有的一个特征.(请将答案按下列要求写在横线上:特征不能用否定形式表述,点用字母表示.)
①甲类含两个点,乙类合其余四个点.
甲类:点______,______是同一类点,其特征是______.
乙类:点______,______,______,______,是同一类点,其特征是______.
②甲类合三个点,乙类合其余三个点.
甲类:点______,______,______是同一类点,其特征是______.
乙类:点______,______,______是同一类点,其特征是______.(2)判断下列命题是否正确,正确的在括号内打“√”,并说明理由;
错误的在括号内打“×”,并举反例说明.
①直线y=-2x+11与线段AD没有交点______;(如需要,可在坐标系上作出示意图)

②直线y=-2x+11将四边形ABCD分成面积相等的两部分______.

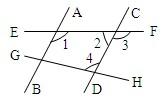 6、已知:如图,下面判定正确的是( )
6、已知:如图,下面判定正确的是( )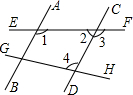 已知:如图,下面判定正确的是
已知:如图,下面判定正确的是