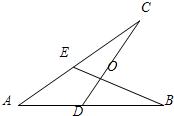21、如图，给出四个等式：①AE=AD；②AB=AC；③OB=OC；④∠B=∠C． 现选取其中的三个，以两个作为已知条件，另一个作为结论组成命题．
（1）请你写出两个真命题（用序号填空）．
真命题1：已知求证：．
真命题2：已知求证：．
（2）请你选择其中的一个真命题加以证明；
我选择真命题．
证明：

11、如图，在等腰梯形ABCD中，AB∥DC，AD=BC=CD，点E为AB上一点，连接CE．请添加一个你认为合适的条件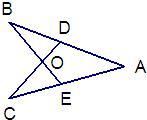，使四边形AECD为菱形．

24、如果，AE=AD，AB=AC，那么△ABE与△ACD是否全等，为什么？

如图，在下面四个条件中：①AE=AD，②AB=AC，③MB=MC，④∠B=∠C．
请你以其中的两个做为条件，第三个做结论，写出一个正确的命题．并说明你的理由．

在△ADE中，AE=AD且∠AED=∠ADE，∠EAD=90°．

（1）如图（1），若EC、DB分别平分∠AED、∠ADE，交AD、AE于点C、B，连接BC．请你判断AB、AC是否相等，并说明理由；
（2）△ADE的位置保持不变，将（1）中的△ABC绕点A逆时针旋转至图（2）的位置，CD、BE相交于O，请你判断线段BE与CD的位置关系及数量关系，并说明理由；
（3）在（2）的条件下，若CD=8，试求四边形CEDB的面积．