练习册

  • 练习册
  • 试题
    16.6 解答题 【查看更多】

     

    题目列表(包括答案和解析)

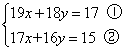    、阅读下面解方程组的方法，然后回答有关问题：

    解方程组时，如果直接消元，那将是很繁琐的，采用下面的解法则会简便许多．

    解：①－②，得 ，即    ③

    ③×16，得   ④

    ②－④，得，从而       ∴方程组的解为               

     请你采用上述方法解方程组：

    并猜测关于的方程组的解是什么？并利用方程组的解加以验证．

    查看答案和解析>>

    阅读并解答：
    先阅读下列计算方法：某商店将甲乙两种糖果混合销售，并按以下公式确定混合糖果的单价：单价=
    a1m1+a2m2m1+m2
    （元/千克），其中m1、m2分别为甲乙两种糖果的重量（千克），a1、a2分别为甲乙两种糖果的单价（元/千克）．
    再解答下列问题：已知甲种糖果单价为20元/千克，乙种糖果单价为16元/千克．
    （1）现将10千克乙种糖果和一箱甲种糖果混合（搅拌均匀）销售，已知混合糖果的单价为18.4元/千克，问：这箱甲种糖果有多少千克？
    （2）现将10千克乙种糖果和一箱甲种糖果混合（搅拌均匀）销售，售出5千克后，又在混合糖果中加入5千克乙种糖果，再出售时，混合糖果的单价为17.5元/千克．问：这箱甲种糖果有多少千克？

    查看答案和解析>>

    观察、分析下面两个例题的计算方法：
    例1：计算：（1
    3
    4
    -
    7
    8
    -
    7
    12
    ）÷（-
    7
    8
    ）+（-2）÷
    3
    4

    解：原式=（1
    3
    4
    -
    7
    8
    -
    7
    12
    ）×（-
    8
    7
    ）+（-2）÷
    3
    4
    ①
    =
    7
    4
    ×（-
    8
    7
    ）+（-
    7
    8
    ）×（-
    8
    7
    ）+（-
    7
    12
    ）×（-
    8
    7
    ）+（-2）×
    4
    3
    ②
    =-2+1+
    2
    3
    -
    8
    3
    =-3
    例2：计算：-1-[1-（1-0.5×
    1
    3
    ）]×[2-（-3）2]
    解：原式=-1-[1-（1-
    1
    6
    ）]×（2-9）③
    =-1-（1-1+
    1
    6
    ）×（2-9）④
    =-1-
    1
    6
    ×（-7）=-1+
    7
    6
    =
    1
    6
    ．
    请回答以下问题：
    （1）有理数的混合运算，运算顺序是如何规定的？
    （2）例1中，步骤①到②，比先算括号里的简便吗？用的什么方法？
    （3）例2中，步骤③到④，比先算括号里的简便吗？用的什么方法？
    （4）学完“有理数”这一章后，你增长了哪些知识和能力？

    查看答案和解析>>

    为了解某品牌A、B两种型号冰箱的销售状况，王明对其专卖店开业以来连续七个月的销售情况进行了统计，并将得到的数据制作成如下的统计表：
    月份 一月 二月 三月 四月 五月 六月 七月
    A型销售量（台） 10 14 17 16 13 14 14
    B型销售量（台） 6 10 14 15 16 17 20
    请用你所学过的有关统计的知识（平均数、中位数、方差和极差）回答下列问题：
    （1）两种型号的冰箱有哪些相同点和不同点；
    （2）请你根据七个月的销售情况，对专卖店的今后进货情况提出建议．

    查看答案和解析>>

    为了解某市初中九年级学生科学实验测评成绩情况，现从中抽取部分学生的实验测评成绩统计如表一、表二所示．
    表一
    成绩（分）012345678910
    人数20021131619
    成绩（分）11121314151617181920
    人数171315162080100120200380
    表二
    组别频数频率
    0～20.2%
    3～54
    6～880.8%
    9～11424.2%
    12～14444.4%
    15～1720020%
    18～2070070%
    根据上面提供的信息，回答下列问题：
    （1）将表一、表二中的空格部分补充完整．
    （2）将学生的成绩分成三个等级，总分为20分，其中17～20分为A，10～16分为P，0～9分为E，那么被抽取的这部分学生中得A、P、E三个等级的比例分别是多少？
    （3）已知该市初中九年级参加科学实验测评的学生共有16000名，请估计该市初中九年级学生实验测评成绩达到A的人数约为多 少？

    查看答案和解析>>


    同步练习册答案