
题目列表(包括答案和解析)
如图,在平面直角坐标系中,有一Rt△ABC,且A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转得到的.
【小题1】请写出旋转中心的坐标是 ,旋转角是 度;
【小题2】以(1)中的旋转中心为中心,分别画出△A1AC1顺时针旋转90°、180°的三角形;
【小题3】设Rt△ABC两直角边BC=a、AC=b、斜边AB=c,利用变换前后所形成的图案证明勾股定理.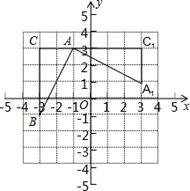

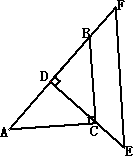
(1)已知:有两块完全相同的含45°角的三角板,如图,将Rt△DEF的直角的=顶点D放在Rt△ABC斜边AB的中点处,这时两块三角板重叠部分△DBC的面积是△ABC的面积的________;
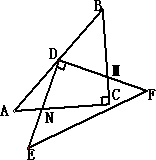
(2)如图,点D不动,将Rt△DEF绕着顶点D旋转α(0°<∠α<90°),这时两块三角板重叠部分为任意四边形DNCM,这时四边形DNCM的面积是△ABC的面积的________;
(3)若Rt△DEF的顶点D在AB上移动(不与点A、B重合),且两条直角边与Rt△ABC的两条直角边相交,是否存在一点,使得两块三角板重叠部分的面积是Rt△ABC的面积的![]() ,如果存在,请在图中画出此时的图形,并说明点D在AB上的位置.如果不存在,说明理由.
,如果存在,请在图中画出此时的图形,并说明点D在AB上的位置.如果不存在,说明理由.
(1)已知:有两块完全相同的含45°角的三角板,如图,将Rt△DEF的直角的=顶点D放在Rt△ABC斜边AB的中点处,这时两块三角板重叠部分△DBC的面积是△ABC的面积的________;

(2)如图,点D不动,将Rt△DEF绕着顶点D旋转α(0°<∠α<90°),这时两块三角板重叠部分为任意四边形DNCM,这时四边形DNCM的面积是△ABC的面积的________;
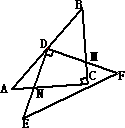
(3)若Rt△DEF的顶点D在AB上移动(不与点A、B重合),且两条直角边与Rt△ABC的两条直角边相交,是否存在一点,使得两块三角板重叠部分的面积是Rt△ABC的面积的![]() ,如果存在,请在图中画出此时的图形,并说明点D在AB上的位置.如果不存在,说明理由.
,如果存在,请在图中画出此时的图形,并说明点D在AB上的位置.如果不存在,说明理由.
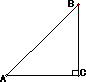
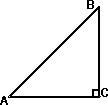
如图,在Rt△ABC中,∠C=90°,两直角边AC、BC的长恰是方程x2-4x+2=0的两个不同的根,则Rt△ABC的斜边上的高线CD的长为

A.![]()
B.![]()
C.![]()
D.2![]()
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com