
题目列表(包括答案和解析)
| 售价x (元) | … | 60 | 65 | 70 | 75 | 80 |
| 月销量y (万箱) | … | 6 | 5.5 | 5 | 4.5 | 4 |
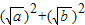 =
= -
-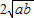 +
+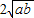 =
=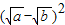 +
+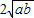 ,
, ≥0,∴
≥0,∴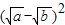 +
+ ≥0+
≥0+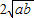 ,即a+b≥
,即a+b≥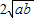 .
. (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥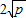 ,当且仅当a、b满足______时,a+b有最小值
,当且仅当a、b满足______时,a+b有最小值 .
.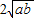 成立,并指出等号成立时的条件.
成立,并指出等号成立时的条件. 的图象上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连接DF、EF,求四边形ADFE面积的最小值.
的图象上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连接DF、EF,求四边形ADFE面积的最小值.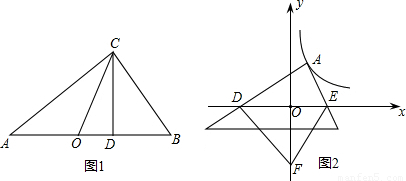
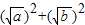 =
=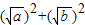 -
-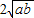 +
+ =
= +
+ ,
,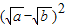 ≥0,∴
≥0,∴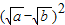 +
+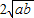 ≥0+
≥0+ ,即a+b≥
,即a+b≥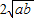 .
. (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥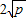 ,当且仅当a、b满足______时,a+b有最小值
,当且仅当a、b满足______时,a+b有最小值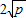 .
.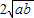 成立,并指出等号成立时的条件.
成立,并指出等号成立时的条件.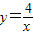 的图象上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连接DF、EF,求四边形ADFE面积的最小值.
的图象上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连接DF、EF,求四边形ADFE面积的最小值.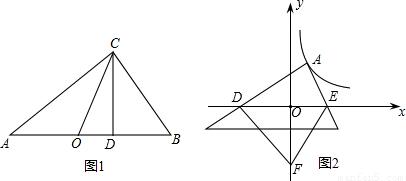
 =
= -
-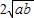 +
+ =
=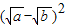 +
+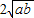 ,
, ≥0,∴
≥0,∴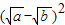 +
+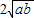 ≥0+
≥0+ ,即a+b≥
,即a+b≥ .
. (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥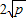 ,当且仅当a、b满足______时,a+b有最小值
,当且仅当a、b满足______时,a+b有最小值 .
.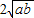 成立,并指出等号成立时的条件.
成立,并指出等号成立时的条件.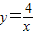 的图象上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连接DF、EF,求四边形ADFE面积的最小值.
的图象上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连接DF、EF,求四边形ADFE面积的最小值.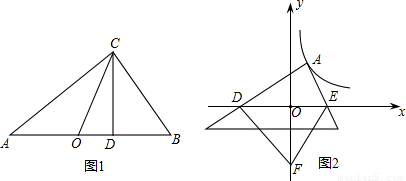
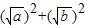 =
=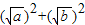 -
-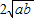 +
+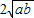 =
=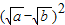 +
+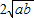 ,
,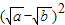 ≥0,∴
≥0,∴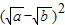 +
+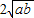 ≥0+
≥0+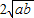 ,即a+b≥
,即a+b≥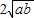 .
.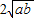 (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥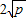 ,当且仅当a、b满足______时,a+b有最小值
,当且仅当a、b满足______时,a+b有最小值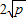 .
.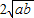 成立,并指出等号成立时的条件.
成立,并指出等号成立时的条件.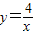 的图象上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连接DF、EF,求四边形ADFE面积的最小值.
的图象上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连接DF、EF,求四边形ADFE面积的最小值.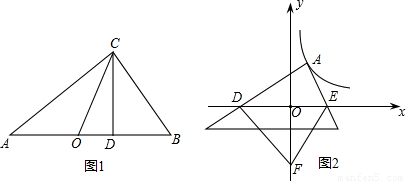
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com