
题目列表(包括答案和解析)
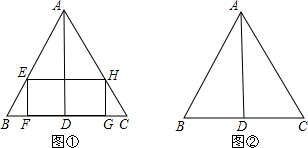

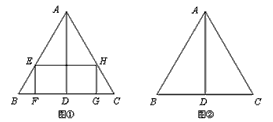
如图,已知等边三角形ABC的边长为2,AD是BC边上的高.
⑴在△ABC内部作一个矩形EFGH(如图①),其中E、H分别在边AB、AC上,FG在边BC上.
① 设矩形的一边FG=x,那么EF= ▲ .(用含有x的代数式表示)
② 设矩形的面积为y,当x取何值时,y的值最大?最大值是多少?
⑵当矩形EFGH面积最大时,请在图②中画出此时点E的位置.(要求尺规作图,保留作图痕迹,并简要说明确定点E的方法)
 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com