
题目列表(包括答案和解析)
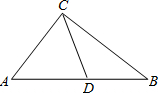 阅读:定理“直角三角形斜边上的中线等于斜边的一半”,如图,Rt△ABC中,D为AB中点,则CD=AD=BD=
阅读:定理“直角三角形斜边上的中线等于斜边的一半”,如图,Rt△ABC中,D为AB中点,则CD=AD=BD=| 1 | 2 |
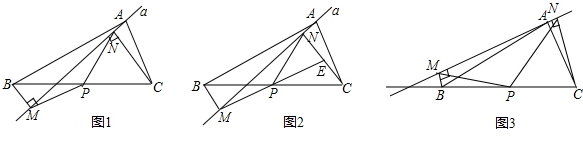
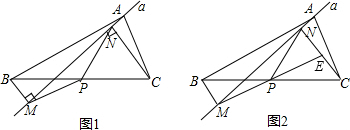
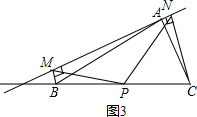
如图1,在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若B、P在直线a的异侧, BM^直线a于点M,CN^直线a于点N,连接PM、PN;
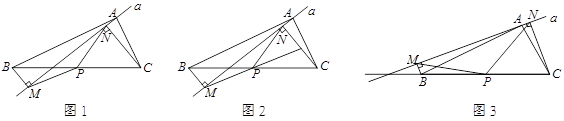 (1)延长MP交CN于点E(如图2)。j 求证:△BPM@△CPE;k 求证:PM = PN;
(1)延长MP交CN于点E(如图2)。j 求证:△BPM@△CPE;k 求证:PM = PN;
(2) 若直线a绕点A旋转到图3的位置时,点B、P在直线a的同侧,其它条件不变。此时PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由;
(3) 若直线a绕点A旋转到与BC边平行的位置时,其它条件不变。请直接判断四边形MBCN
的形状及此时PM=PN还成立吗?不必说明理由。
 (1) 延长MP交CN于点E(如图2)。j求证:△BPM@△CPE;k求证:PM = PN;
(1) 延长MP交CN于点E(如图2)。j求证:△BPM@△CPE;k求证:PM = PN;如图1,在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若B、P在直线a的异侧,BM^直线a于点M,CN^直线a于点N,连接PM、PN
1.延长MP交CN于点E(如图2)。j 求证:△BPM@△CPE;k 求证:PM = PN;
2.若直线a绕点A旋转到图3的位置时,点B、P在直线a的同侧,其它条件不变。此时PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由;
3.若直线a绕点A旋转到与BC边平行的位置时,其它条件不变。请直接判断四边形MBCN的形状及此时PM=PN还成立吗?不必说明理由。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com