题目列表(包括答案和解析)
将一个分数的分子、分母同时加上一个正数，这个分数变大了吗？先用一组具体的数来做一些试验：
→
→
→
→
－
→－
－
→－
(1)当这个分数是正的真分数时，分数变大；
(2)当这个分数是正的假分数时，分数变小；
(3)当这个分数是负分数时，结论刚好与上述相反．
以上结论是通过一些具体的数归纳出来的，但是我们不可能把所有数都拿出来一一验证这些结论是否正确．因此，在数学中把这种未经严格证明而只是从一些具体的数中归纳出来的规律，叫做“猜想”．猜想可能是对的，也可能是错的．要肯定上述结论是对的，必须用字母表示任意的数，利用代数式来证明它们．你能证明上述结论吗？
如图，在平面直角坐标系中，两个函数y＝x，y＝－
x＋6的图象交于点A. 动点P从点O开始沿OA方向以每秒1个单位的速度运动，作PQ∥x轴交直线BC于点Q，以PQ为一边向下作正方形PQMN，设它与△OAB重叠部分的面积为S．
(1)求点A的坐标；
(2)试求出点P在线段OA上运动时，S与运动时间t(秒)的关系式；
(3)在(2)的条件下，S是否有最大值？若有，求出t为何值时，S有最大值，并求出最大值；若没有，请说明理由；
(4)若点P经过点A后继续按原方向、原速度运动，当正方形PQMN与△OAB重叠部分面积最大时，运动时间t满足的条件是什么．
图a是一个长为2m、宽为2n的长方形，现在沿图中虚线剪开，平均分成四块全等的小长方形，然后按图b的形状拼成一个正方形．
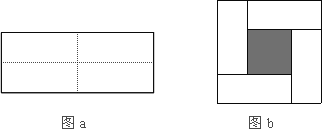
(1)你认为图b中的阴影部分的正方形的边长等于多少？
(2)观察图b你能写出下列三个代数式之间的等量关系吗？代数式：(m＋n)2，(m－n)2，mn．
(3)根据(2)题中的等量关系，解决如下问题：若a＋b＝7，ab＝10，求a－b的值．
(4)如下图，现有正方形甲2张，正方形乙2张，长方形丙5张，请你将它们组合拼成一个大长方形(画出图示)，并运用面积之间的关系，将多项式2a2＋5ab＋2b2分解因式．
如图，在直角坐标系中，梯形ABCD的底边AB在x轴上，底边CD的端点D在y轴上.直线CB的表达式为
，点A、D的坐标分别为（－4，0），（0，4）. 动点P从A点出发，在AB边上匀速运动. 动点Q从点B出发，在折线BCD上匀速运动，速度均为每秒1个单位长度. 当其中一个动点到达终点时，另一动点也停止运动. 设点P运动t（秒）时，△OPQ的面积为S（不能构成△OPQ的动点除外）.
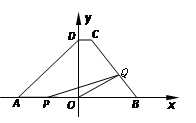
1.求出点C的坐标
2.求S随t变化的函数关系式；
3.当t为何值时，S有最大值？并求出这个最大值
如图，在直角坐标系中，梯形ABCD的底边AB在x轴上，底边CD的端点D在y轴上.直线CB的表达式为y=－
x+
，点A、D的坐标分别为（－4，0），（0，4）.动点P自A点出发，在AB上匀速运行.动点Q自点B出发，在折线BCD上匀速运行，速度均为每秒1个单位.当其中一个动点到达终点时，它们同时停止运动.设点P运动t（秒）时，△OPQ的面积为s（不能构成△OPQ的动点除外）.
1.求出点B、C的坐标；
2.求s随t变化的函数关系式；
3.当t为何值时s有最大值？并求出最大值.
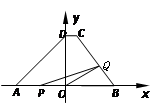
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com