若关于X的分式方程的解为负数，则的取值范围是（      ）

      A、＜－5         B、＞－5          C、＜－5且≠1            D、＞－5且≠－1 

若关于X的分式方程的解为负数，则的取值范围是（      ）

   A、＜－5     B、＞－5      C、＜－5且≠1       D、＞－5且≠－1 

解方程x²＋4x－5＝0，除因式分解法、配方法、公式法以外，还可采用如下解法：

解：由原方程可知x＝1是方程x²＋4x－5＝0的根．

设方程的另一个根为x₀，则由一元二次方程根与系数的关系可知：1×x₀＝－5，∴x₀＝－5，依照上述解法，请解方程：

(1)x²－(＋)x＋＝0；(2)x＋＝a＋

(3)根据(2)的结果，你能否猜出方程x＋＝a＋的根是多少？

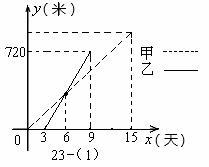
(1) A、B两村之间的公路进行对接修筑，甲工程队从A村向B村方向修筑，乙工程队从B村向A村方向修筑．已知甲工程队先施工3天，乙工程队再开始施工．乙工程队施工几天后因另有任务提前离开，余下的任务由甲工程队单独完成，直到公路修通．下图23－（1）是甲乙两个工程队修公路的长度y（米）与施工时间x（天）之间的函数图象，请根据图象所提供的信息解答下列问题：

①乙工程队每天修公路多少米？

②分别求甲、乙工程队修公路的长度y（米）与施工时间x（天）之间的函数关系式；

③若乙工程队后来进入施工后，不提前离开，直到公路对接完工，那么施工过程共需几天？

（2）如图23－（2），直线分别与x轴、y轴交于点A、B，在第一象限取点C，使△ABC成为等腰直角三角形；如果在第二象限内有一点P（a， ），使△ABP的面积与Rt△ABC的面积相等，求a的值.

用“拆项法”解分式方程

　　大家知道，解分式方程的基本方法是，把方程的两边同乘以各分母的最简公分母，化为整式方程来解，而对于一些特殊的分式方程来说，采用上述方法往往越解越繁．下面我们介绍一种简捷、明快的方法－－拆项法．

　　例：解方程

　　解：先降低方程中各分式分子的次数，将原方程变形为

　　即(4＋)－(7＋)＝(1－)－(4－)

　　整理得

　　两边各自通分得

　　

　　∴(x－2)(x－1)＝(x－7)(x－6)

　　即x²－3x＋2＝x²－13x＋42

　　也即10x＝40　　∴x＝4

　　经检验知，x＝4是原方程的根．

请你运用上述方法，解分式方程