练习册

  • 练习册
  • 试题
    15．如右图.在⊙O中.AB为直径.∠ACB的平分线交⊙O于D. 则∠ABD= °. 【查看更多】

     

    题目列表(包括答案和解析)

    如图①，直线AM⊥AN，⊙O分别与AM、AN相切于B、C两点，连结OC、BC，则有∠ACB＝∠OCB；(请思考：为什么？)如果测得AB＝a，则可知⊙O的半径r＝a．(请思考：为什么？)

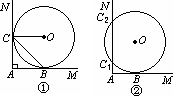
    (1)将图①中直线AN向右平移，与⊙O相交于C1、C2两点，⊙O与AM的切点仍记为B，如图②．请你写出与平移前相应的结论，并将图②补充完整；判断此结论是否成立，且说明理由．

    (2)在图②中，若只测得AB＝a，能否求出⊙O的半径r？若能求出，请你用a表示r；若不能求出，请补充一个条件(补充条件时不能添加辅助线，若补充线段请用b表示，若补充角请用α表示)，并用a和补充的条件表示r．

    查看答案和解析>>

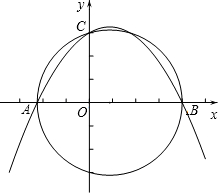    精英家教网如图所示，在平面直角坐标系xOy中，已知点A（-
    94
    ，0），点C（0，3），点B是x轴上一点（位于点A的右侧），以AB为直径的圆恰好经过点C．
    （1）求∠ACB的度数；
    （2）已知抛物线y=ax2+bx+3经过A、B两点，求抛物线的解析式；
    （3）线段BC上是否存在点D，使△BOD为等腰三角形？若存在，则求出所有符合条件的点D的坐标；若不存在，请说明理由．

    查看答案和解析>>

    如图所示，在平面直角坐标系O中xy，已知点A（-，0），点C（0，3），点B是x轴上一点（位于点A的右侧），以AB为直径的圆恰好经过点C。
    （1）求∠ACB的度数；
    （2）已知抛物线线y=ax2+bx+3过A、B两点，求抛物线的解析式；
    （3）线段BC上是否存在点D，使△BOD为等腰三角形，若存在，则求出所有符合条件的点D的坐标；若不存在，请说明理由。

    查看答案和解析>>

    如图所示，在平面直角坐标系Oxy中，已知点A（，0），点C（0,3）点B是x轴上一点（位于点A右侧），以AB为直径的圆恰好经过点C。

    （1）求角ACB的度数；

    （2）已知抛物线y=ax2+bx+3经过A，B两点，求抛物线的解析式；

    （3）线段BC上是否存在点D，使△BOD为等腰三角形？若存在，则求出所有符合条件的点D的坐标；若不存在，请说明理由。

                                 

    查看答案和解析>>

    如图，在Rt△ABC中，∠ACB=90°，AC=6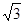cm ，BC=6cm，经过A，B的直线l以1cm/秒的速度向下作匀速平移运动，交BC于点B′，交CD于点 D′，与此同时，点P从点B′ 出发，在直线l上以1cm/秒的速度沿直线l向右下方向作匀速运动．设它们运动的时间为t秒．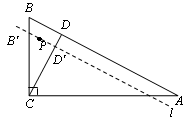

    （1）你求出的AB的长是　　　　　；
    （2）过点C作CD⊥AB于点D，t为何值时，点P移动到CD上？
    （3）t为何值时，以点P为圆心、1cm为半径的圆与直线CD相切？
    （4）以点P为圆心、1 cm为半径的⊙P与CD所在的直线相交时，是否存在点P与两个交点构成的三角形是等边三角形？若存在，直接写出t的值；若不存在，说明理由.

    查看答案和解析>>


    同步练习册答案