用一块边长为60cm的正方形薄钢片制作一个长方体盒子：
（1）如果要做成一个没有盖的长方体盒子，可先在薄钢片的四个角上截去四个相同的小正方形（如图1），然后把四边折合起来（如图2）；
①求做成的盒子底面积y（cm²）与截去小正方形边长x（cm）之间的函数关系式；
②当做成的盒子的底面积为900cm²时，试求该盒子的容积．
（2）如果要做成一个有盖的长方体盒子，制作方案要求同时符合下列两个条件：
①必须在薄钢片的四个角上各截去一个四边形；（其余部分不能裁截）
②折合后薄钢片既无空隙又不重叠地围成各盒面．
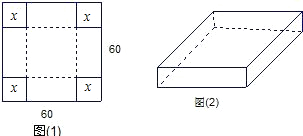
请你画出符合上述制作方案的一种草图（不必说明画法与根据）；并求当底面积为800cm²时，该盒子的高．

用一块边长为60cm的正方形薄钢片制作一个长方体盒子：

(1)如果要做成一个没有盖的长方体盒子，可先在薄钢片的四个角上截去四个相同的小正方形(如图A)，然后把四边折合起来(如图B)．

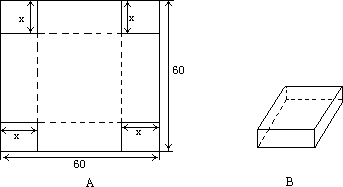
①求做成的盒子底面积y(cm²)与截去小正方形边长x(cm)之间的函数关系式；

②当做成的盒子的底面积为900cm²时，试求该盒子的容积．

(2)如果要做成一个有盖的长方体盒子，其制作方案要求同时符合下列两个条件：

①必须在薄钢片的四个角上各截去一个四边形(其余部分不能裁截)；

②折合后薄钢片既无空隙、又不重叠地围成各盒面．

请你画出符合上述制作方案的一种草图(不必说明画法与根据)；并求当底面积为800cm²时，该盒子的高．

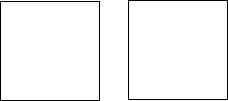
如图：一正方形纸片，根据要求进行多次分割，把它分割成若干个直角三角形．具体操作过程如下：第一次分割：将正方形纸片分成4个全等的直角三角形；第二次分割：将上次得到的直角三角形中的一个再分成4个全等的直角三角形；以后按第二次分割的方法重复进行．

1.请你设计出两种符合题意的分割方案（分割3次）；

2.设正方形的边长为a，请你通过对其中一种方案的操作和观察，将第二、第三次分割后所得的最小的直角三角形的面积S填入下表：

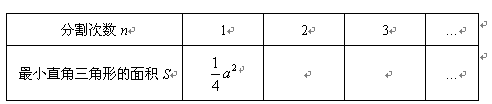
3.在条件（2）下，请你猜想：分割所得的最小直角三角形面积S与分割次数n有什么关系？用数学表达式表示出来．