
题目列表(包括答案和解析)
(本题满分10分)将一箱苹果分给若干个小朋友,若每位小朋友分5个苹果,则还剩12个苹果;若每位小朋友分8个苹果,则有一个小朋友分不到8个苹果。求这一箱苹果的个数与小朋友的人数。
.(本题满分8分)
有一个不透明口袋,装有分别标有数字1,2,3,4的4个小球(小球除数字不同外,其余都相同),另有3张背面完全一样、正面分别写有数字1,2,3的卡片.小敏从口袋中任意摸出一个小球,小颖从这3张背面朝上的卡片中任意摸出一张,然后计算小球和卡片上的两个数的和.请你用列表或画树状图的方法,求摸出的这两个数的和为5的概率.
(本题满分12分)有这样一道习题:已知:如图1,OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点(不与O、A重合),BP的延长线交⊙O于Q,R是OA的延长线上一点,且RP=RQ.说明:RQ为⊙O的切线. (无须证明)
请探究下列变化:
变化一:交换题设与结论.
如图1,已知OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点(不与O、A重合),BP的延长线交⊙O于Q,过Q点作⊙O的切线交OA的延长线于R.说明:RP=RQ.(要证明)
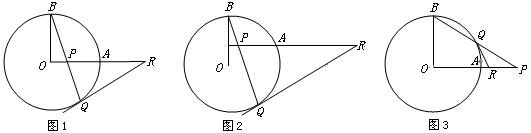
变化二:运动探求.
(1)如图2,若OA向上平移,变化一中的结论还成立吗?(只需交待判断) 答:_________.
(2)如图3,如果P在OA的延长线上时,BP交⊙O于Q,过点Q作⊙O的切线交OA的延长线于R,变化一中的结论还成立吗?为什么? 来]
(本题满分10分)有四张背面相同的纸牌A,B,C,D,其正面分别画有四个不同的几何图形(如图).小明将这4张纸牌背面朝上洗匀后摸出一张,将剩余3张洗匀后再摸出一张.
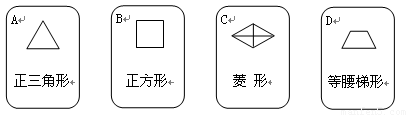
1.(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌用A,B,C,D表示);
2.(2)求摸出的两张牌面图形既是轴对称图形又是中心对称图形纸牌的概率.
(本题满分10分)将一箱苹果分给若干个小朋友,若每位小朋友分5个苹果,则还剩12个苹果;若每位小朋友分8个苹果,则有一个小朋友分不到8个苹果。求这一箱苹果的个数与小朋友的人数。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com