
题目列表(包括答案和解析)
(本题满分14分,第(1)小题满分4分,第(2)、(3)小题满分各5分)在Rt△ABC中,∠ACB=90°,BC=30,AB=50.点P是AB边上任意一点,直线PE⊥AB,与边AC或BC相交于E.点M在线段AP上,点N在线段BP上,EM=EN,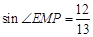 .
.
(1)如图1,当点E与点C重合时,求CM的长;
(2)如图2,当点E在边AC上时,点E不与点A、C重合,设AP=x,BN=y,求y关于x的函数关系式,并写出函数的定义域;
(3)若△AME∽△ENB(△AME的顶点A、M、E分别与△ENB的顶点E、N、B对应),求AP的长.
(2011广西崇左,24,14分)(本小题满分14分)如图,在边长为8的正方形ABCD
中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点M,连接OM,过点M作圆O的切线交边BC于点N.
(1) 求证:△ODM∽△MCN;
(2) 设DM=x,求OA的长(用含x的代数式表示);
(3) 在点O运动的过程中,设△CMN的周长为p,试用含x的代数式表示p,你能发现怎样的结论?
(2011广西崇左,24,14分)(本小题满分14分)如图,在边长为8的正方形ABCD
中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点M,连接OM,过点M作圆O的切线交边BC于点N.
(1) 求证:△ODM∽△MCN;
(2) 设DM=x,求OA的长(用含x的代数式表示);
(3) 在点O运动的过程中,设△CMN的周长为p,试用含x的代数式表示p,你能发现怎样的结论?
(本题满分14分,第(1)、(2)小题每小题满分5分,第(3)小题满分4分)
已知,在边长为6的正方形ABCD的两侧如图作正方形BEFG、正方形DMNK,恰好使得N、A、F三点在一直线上,联结MF交线段AD于点P,联结NP,设正方形BEFG的边长为x,正方形DMNK的边长为y,
(1)求y关于x的函数关系式及自变量x的取值范围;
(2)当△NPF的面积为32时,求x的值;
(3)以P为圆心,AP为半径的圆能否与以G为圆心,GF为半径的圆相切,若能请求x的值,若不能,请说明理由。

(本题满分14分,第(1)小题4分,第(2)小题①6分、第(2)小题②4分)
直角三角板ABC中,∠A=30°,BC=1.将其绕直角顶点C逆时针旋转一个角![]() (
(![]() 且
且![]() ≠ 90°),得到Rt△
≠ 90°),得到Rt△![]() ,
,
(1)如图9,当![]() 边经过点B时,求旋转角
边经过点B时,求旋转角![]() 的度数;
的度数;
(2)在三角板旋转的过程中,边![]() 与AB所在直线交于点D,过点 D作DE∥
与AB所在直线交于点D,过点 D作DE∥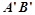 交
交![]() 边于点E,联结BE.
边于点E,联结BE.
①当![]() 时,设
时,设![]() ,
,![]() ,求
,求![]() 与
与![]() 之间的函数解析式及定义域;
之间的函数解析式及定义域;
②当![]() 时,求
时,求![]() 的长.
的长.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com