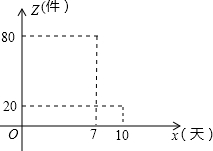进入三月以来，重庆的气温渐渐升高，羽绒服进入了销售淡季．为此重庆某百货公司对某品牌的A款羽绒服进行了清仓大处理．已知A款羽绒服的销售价格y元与第x天（1≤x≤10，且为整数）之间的关系可用如下表表示：

时间（x天）	1	2	3	4	5	6	7	8	9	10
售价y（元/件）	550	500	450	400	350	300	300	300	300	300

在销售的前6天，A款羽绒服的销售数量z₁（件）与第x天的关系式为z₁=20x+40（1≤x≤6且为整数）；后4天（7≤x≤10，且为整数）的销售数量z₂件与第x天的关系如图所示
（1）请观察题中表格，用所学过的一次函数、反比例函数或二次函数的有关知识，直接写出y与x之间的函数关系式，根据如图所示的变化趋势，直接写出z₂与x之间的一次函数关系式．
（2）若A款羽绒服的进价为每件200元，该专柜共有5个员工，每位员工每天的工资为100元，该专柜每天所需的固定支出为1000元，请结合上述信息，求这10天内哪天的利润最大，并求出这个最大利润．
（3）在第（2）问的前提下，为了提高收益、减少库存，商场在第11天作出以下决定：第11-15天继续维持A款羽绒服的售价，结果每天的销售量均与第10天的持平，同时在第11-15天将B款羽绒服也作为促销商品，而且作为销售重点，已知B款羽绒服的进价仍为200元每件，销售价格比A款羽绒服取得最大利润当天的售价降低了a%，而每天销售量则比第10天A款羽绒服的销量提高了2a%，最后5天A、B两款羽绒服的总利润为27100元，请你参考以下数据，计算出a的值．
参考数据：2.5²=6.25，2.6²=6.76，2.7²=7.29，2.8²=7.84．

（2012•宁波）为了鼓励市民节约用水，某市居民生活用水按阶梯式水价计费．如表是该市居民“一户一表”生活用水及提示计费价格表的部分信息：

自来水销售价格		污水处理价格
每户每月用水量	单价：元/吨	单价：元/吨
17吨以下	a	0.80
超过17吨但不超过30吨的部分	b	0.80
超过30吨的部分	6.00	0.80

（说明：①每户产生的污水量等于该户自来水用水量；②水费=自来水费用+污水处理费用）
已知小王家2012年4月份用水20吨，交水费66元；5月份用水25吨，交水费91元．
（1）求a、b的值；
（2）随着夏天的到来，用水量将增加．为了节省开支，小王计划把6月份的水费控制在不超过家庭月收入的2%．若小王家的月收入为9200元，则小王家6月份最多能用水多少吨？

22、某企业用10辆相同的汽车将一批救灾物资运到玉树，每辆汽车能装8吨甲种救灾物资，或10吨乙种救灾物资，或11吨丙种救灾物资，规定每辆车只能装同一种救灾物资，而且必须 满载．已知运送了甲、乙、丙三种救灾物资00吨，且每种救灾物资不少于一车．
（1）设用x辆车装甲种救灾物资，y辆车装乙种救灾物资，求y与x之间的函数关系式，并写 出自变量x的取值范围；
（2）若运送三种苹果所获利润的情况如下表所示：

品种救灾物资	甲	乙	丙
每吨救灾物资所需费用（万元）	0.22	0.21	0.2

 设此次运输的费用为W（万元），问：如何安排车辆分配方案才能使运输W费用最小？并求出最小费用．