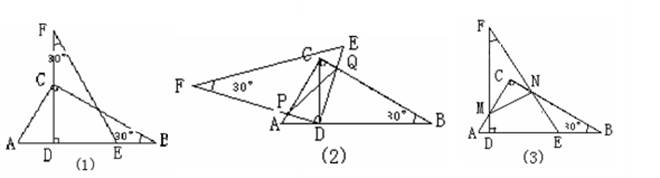
如图（1），我们将相同的两块含30°角的直角三角尺Rt△DEF与Rt△ABC叠合，使DE在AB上，DF过点C，已知AC=DE=6。将图（1）中的△DEF绕点D逆时针旋转（DF与AB不重合），使边DF、DE分别交AC、BC于点P、Q，如图（2）。
(1)求证：△CQD∽△APD
(2)连结PQ，设AP=x，求面积S_△PCQ关于x的函数关系式；
(3)将图（1）中的△DEF 向左平移（A、D不重合），使边FD、FE分别交AC、BC于点M、N，如图（3）,连结MN，试问△MCN面积是否存在最大值、如不存在，请说明理由；如存在请求出S_△MCN 的最大值，

如图（1），我们将相同的两块含30°角的直角三角尺Rt△DEF与Rt△ABC叠合，使DE在AB上，DF过点C，已知AC=DE=6。将图（1）中的△DEF绕点D逆时针旋转（DF与AB不重合），使边DF、DE分别交AC、BC于点P、Q，如图（2）。

(1)求证：△CQD∽△APD

(2)连结PQ，设AP=x，求面积S_△PCQ 关于x的函数关系式；

(3)将图（1）中的△DEF 向左平移（A、D不重合），使边FD、FE分别交AC、BC于点M、N，如图（3）,连结MN，试问△MCN面积是否存在最大值、如不存在，请说明理由；如存在请求出S_△MCN 的最大值，

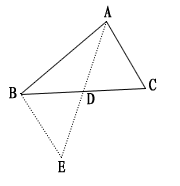
 已知△ABC中，∠C=90°，AC=BC=2，

（1）如图1，如果点D，点E分别在边AC，BC上移动，在移动过程中保持CD=BE, 请判断△PDE的形状（无需说明理由）

（2）如图2，如果点D,点E分别在AC，CB的延长线上移动，在移动过程中仍保持CD=BE，请问：（1）中的结论是否仍成立？若成立，请给予证明；若不成立，请说明理由。

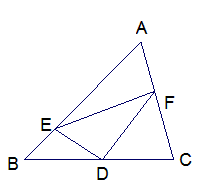
（3）如图3，将一块与△ABC全等的三角板如图放置（DE边与CB边重合），现将三角板绕点C顺时针旋转，当DF边与CA边重合时停止，不考虑起始和结束时情形，设DE，DF

（或它们的延长线）分别交AB（或它的延长线）于G，H点（可参考图4），问BG长为多少时，△CGH是等腰三角形？（只需直接写出BG值）