
题目列表(包括答案和解析)
阅读下面的文章,完成文后问题:
光年和纳米在阅读报刊、杂志或科技书刊时,有时我们会看到“光年”“纳米”这两个名称,你知道它们的含义吗?
光年是天文学中使用的距离单位,简记为l.y.,主要用于度量太阳系外天体的距离.1光年是指光在真空中经历一年所走的距离.真空中光速为c=299792.458km/s,而1年≈60×60×24×365.25(秒),故1光年≈299792.458×60×60×24×365.25≈9.46×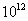 km.
km.
即约等于9.46万亿km.
离太阳最近的恒星(半人马座比邻星)与太阳的距离约为4.22光年.银河系的直径约为10万光年.人类所观测的宇宙速度已达到150亿光年,同学们,你能算出这些距离等于多少km吗?从中你是否可以体会到用光年作单位的优越性?
光年是表示较大距离的一个单位,而纳米则是表示微小距离的单位,简记为nm.1nm=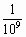 m,即1m=
m,即1m=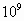 nm.我们通常使用的尺上的一小格是1mm,1mm=
nm.我们通常使用的尺上的一小格是1mm,1mm=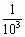 m,可是,1mm=
m,可是,1mm=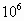 nm,易知1nm相当于1mm的一百万分之一.可想而知,1nm是多么的小.
nm,易知1nm相当于1mm的一百万分之一.可想而知,1nm是多么的小.
当粒子的大小处在1nm~100nm范围内,可称为纳米粒子,纳米粒子的尺寸小,表面积大,具有高度的活性.因此,利用纳米粒子可制备活性极高的催化剂,在火箭固体燃烧中掺入铝的纳米微粒,可提高燃烧效率.利用铁磁纳米材料可制成磁性信用卡、磁性钥匙以及高性能录像带等.利用纳米材料等离子共振频率的可调性可制成隐形飞机的涂料.纳米材料的表面积大,对外界环境(物理的或化学的)十分敏感,在制造传感器方面是很有前途的材料,目前也开发出测量温度、热辐射和检测各种特定气体的传感器,纳米材料在生物和医学中也有重要应用.
纳米材料科学是20世纪80年代末诞生并正在崛起的科技新领域,它将成为跨世纪的科技热点之一.
用科学记数法表示:4.22光年=________km;10万光年=________km;4036m=________nm.
阅读材料:
(1)对于任意两个数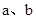 的大小比较,有下面的方法:
的大小比较,有下面的方法:
当 时,一定有
时,一定有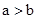 ;
;
当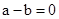 时,一定有
时,一定有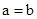 ;
;
当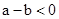 时,一定有
时,一定有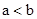 .
.
反过来也成立.因此,我们把这种比较两个数大小的方法叫做“求差法”.
(2)对于比较两个正数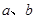 的大小时,我们还可以用它们的平方进行比较:
的大小时,我们还可以用它们的平方进行比较:
∵ ,
,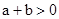
∴( )与(
)与(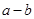 )的符号相同
)的符号相同
当 >0时,
>0时,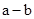 >0,得
>0,得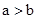
当 =0时,
=0时,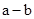 =0,得
=0,得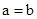
当 <0时,
<0时,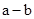 <0,得
<0,得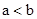
解决下列实际问题:
(1)课堂上,老师让同学们制作几种几何体,张丽同学用了3张A4纸,7张B5纸;李明同学用了2张A4纸,8张B5纸.设每张A4纸的面积为x,每张B5纸的面积为y,且x>y,张丽同学的用纸总面积为W1,李明同学的用纸总面积为W2.回答下列问题:
①W1= (用x、y的式子表示)
W2= (用x、y的式子表示)
②请你分析谁用的纸面积最大.
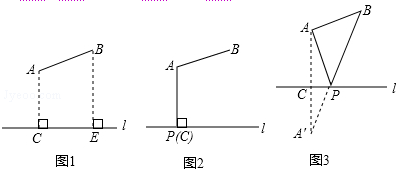
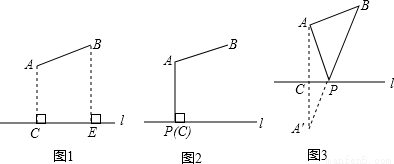
(2)如图1所示,要在燃气管道l上修建一个泵站,分别向A.B两镇供气,已知A.B到l的距离分别是3km、4km(即AC=3km,BE=4km),AB=xkm,现设计两种方案:
方案一:如图2所示,AP⊥l于点P,泵站修建在点P处,该方案中管道长度a1=AB+AP.
方案二:如图3所示,点A′与点A关于l对称,A′B与l相交于点P,泵站修建在点P处,该方案中管道长度a2=AP+BP.
①在方案一中,a1= km(用含x的式子表示);
②在方案二中,a2= km(用含x的式子表示);
③请你分析要使铺设的输气管道较短,应选择方案一还是方案二.
阅读材料:
(1)对于任意两个数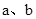 的大小比较,有下面的方法:
的大小比较,有下面的方法:
当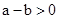 时,一定有
时,一定有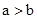 ;
;
当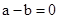 时,一定有
时,一定有 ;
;
当 时,一定有
时,一定有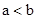 .
.
反过来也成立.因此,我们把这种比较两个数大小的方法叫做“求差法”.
(2)对于比较两个正数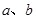 的大小时,我们还可以用它们的平方进行比较:
的大小时,我们还可以用它们的平方进行比较:
∵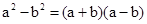 ,
,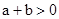
∴(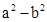 )与(
)与(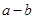 )的符号相同
)的符号相同
当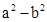 >0时,
>0时,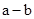 >0,得
>0,得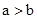
当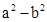 =0时,
=0时,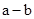 =0,得
=0,得
当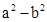 <0时,
<0时,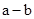 <0,得
<0,得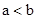
解决下列实际问题:
(1)课堂上,老师让同学们制作几种几何体,张丽同学用了3张A4纸,7张B5纸;李明同学用了2张A4纸,8张B5纸.设每张A4纸的面积为x,每张B5纸的面积为y,且x>y,张丽同学的用纸总面积为W1,李明同学的用纸总面积为W2.回答下列问题:
①W1= (用x、y的式子表示)
W2= (用x、y的式子表示)
②请你分析谁用的纸面积最大.
(2)如图1所示,要在燃气管道l上修建一个泵站,分别向A.B两镇供气,已知A.B到l的距离分别是3km、4km(即AC=3km,BE=4km),AB=xkm,现设计两种方案:
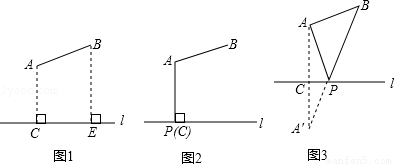
方案一:如图2所示,AP⊥l于点P,泵站修建在点P处,该方案中管道长度a1=AB+AP.
方案二:如图3所示,点A′与点A关于l对称,A′B与l相交于点P,泵站修建在点P处,该方案中管道长度a2=AP+BP.
①在方案一中,a1= km(用含x的式子表示);
②在方案二中,a2= km(用含x的式子表示);
③请你分析要使铺设的输气管道较短,应选择方案一还是方案二.
 阅读材料:(1)对于任意两个数
阅读材料:(1)对于任意两个数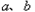 的大小比较,有下面的方法:当
的大小比较,有下面的方法:当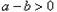 时,一定有
时,一定有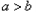 ;当
;当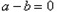 时,一定有
时,一定有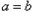 ;当
;当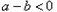 时,一
时,一 定有
定有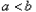 .反过来也成立.因此,我们把这种比较两个数大小的方法叫做“求差法”.
.反过来也成立.因此,我们把这种比较两个数大小的方法叫做“求差法”.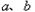 的大小时,我们还可以用它们的平方进行比较:
的大小时,我们还可以用它们的平方进行比较: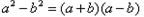 ,
,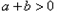
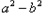 )与(
)与(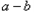 )的符号相同
)的符号相同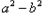 >0时,
>0时,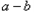 >0,得
>0,得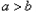
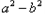 =0时,
=0时,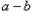 =0,得
=0,得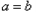
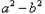 <0时,
<0时,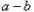 <0,得
<0,得
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com