
题目列表(包括答案和解析)
分式![]() 有意义的条件是________;当x________时,此分式无意义;此分式值为0的条件是________.
有意义的条件是________;当x________时,此分式无意义;此分式值为0的条件是________.
 为了探索代数式
为了探索代数式| x2+1 |
| (8-x)2+25 |
| x2+1 |
| (8-x)2+25 |
| x2+1 |
| (8-x)2+25 |
| 4 |
| 3 |
| 4 |
| 3 |
| x2+4 |
| (12-x)2+9 |
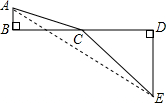
为了探索代数式 的最小值,小明巧妙的运用了“数形结合”思想.具体方法是这样的:如图,C为线段BD上一动点,分别过点B、D作
的最小值,小明巧妙的运用了“数形结合”思想.具体方法是这样的:如图,C为线段BD上一动点,分别过点B、D作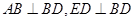 ,连结AC、EC.已知AB=1,DE=5,BD=8,设BC=x.则
,连结AC、EC.已知AB=1,DE=5,BD=8,设BC=x.则 ,
, 则问题即转化成求AC+CE的最小值.
则问题即转化成求AC+CE的最小值.
(1)我们知道当A、C、E在同一直线上时, AC+CE的值最小,于是可求得 的最小值等于 ,此时
的最小值等于 ,此时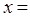 ;
;
(2)请你根据上述的方法和结论,试构图求出代数式 的最小值.
的最小值.
为了探索代数式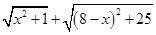 的最小值,
的最小值,
小张巧妙的运用了数学思想.具体方法是这样的:如图,C为线段BD上一动点,分别过点B、D作 ,连结AC、EC.已知AB=1,DE=5,BD=8,设BC=x.则
,连结AC、EC.已知AB=1,DE=5,BD=8,设BC=x.则 ,
, 则问题即转化成求AC+CE的最小值.
则问题即转化成求AC+CE的最小值.

(1)我们知道当A、C、E在同一直线上时,AC+CE的值最小,于是可求得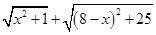 的最小值等于 ,此时
的最小值等于 ,此时 ;
;
(2)题中“小张巧妙的运用了数学思想”是指哪种主要的数学思想?
(选填:函数思想,分类讨论思想、类比思想、数形结合思想)
(3)请你根据上述的方法和结论,试构图求出代数式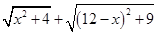 的最小值.
的最小值.
为了探索代数式 的最小值,小明巧妙的运用了“数形结合”思想.具体方法是这样的:如图,C为线段BD上一动点,分别过点B、D作
的最小值,小明巧妙的运用了“数形结合”思想.具体方法是这样的:如图,C为线段BD上一动点,分别过点B、D作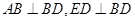 ,连结AC、EC.已知AB=1,DE=5,BD=8,设BC=x.则
,连结AC、EC.已知AB=1,DE=5,BD=8,设BC=x.则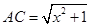 ,
,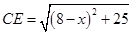 则问题即转化成求AC+CE的最小值.
则问题即转化成求AC+CE的最小值.

(1)我们知道当A、C、E在同一直线上时, AC+CE的值最小,于是可求得 的最小值等于 ,此时
的最小值等于 ,此时 ;
;
(2)请你根据上述的方法和结论,试构图求出代数式 的最小值.
的最小值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com