
题目列表(包括答案和解析)
我们知道顶点在圆上,并且两边都和圆相交的角叫圆周角,因为一条弧所对的圆周角等于它所对的圆心角的一半,而圆心角的度数等于它所对的弧的度数.类似地,我们不妨定义:顶点在圆外,并且两边都和圆相交的角叫圆外角.如图中,∠CAE是圆外角,那么∠CAE的度数与它所夹的两条弧 和
和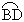 的度数有什么关系?
的度数有什么关系?
(1)把你的猜想用文字表达;
(2)证明你的猜想.

我们知道顶点在圆上,并且两边都和圆相交的角叫圆周角,因为一条弧所对的圆周角等于它所对的圆心角的一半,而圆心角的度数等于它所对的弧的度数.类似地,我们不妨定义:顶点在圆外,并且两边都和圆相交的角叫圆外角.如图中,∠CAE是圆外角,那么∠CAE的度数与它所夹的两条弧 和
和 的度数有什么关系?
的度数有什么关系?
(1)把你的猜想用文字表达;
(2)证明你的猜想.


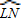 .
.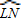 的度数是80,那么∠LMN的度数是______.
的度数是80,那么∠LMN的度数是______.
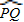 ,∠P=
,∠P=
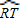 .
.
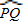 -
-
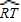 =
= (
(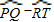 ).
).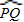 =80°,
=80°,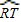 =20°,那么∠O=______°.
=20°,那么∠O=______°.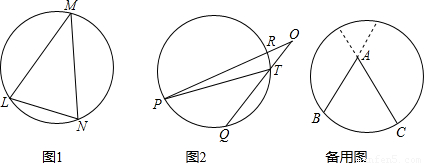

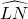 .
.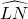 的度数是80,那么∠LMN的度数是________.
的度数是80,那么∠LMN的度数是________.
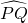 ,∠P=
,∠P=
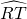 .
.
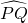 -
-
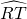 =
= (
(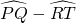 ).
).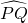 =80°,
=80°,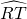 =20°,那么∠O=________°.
=20°,那么∠O=________°.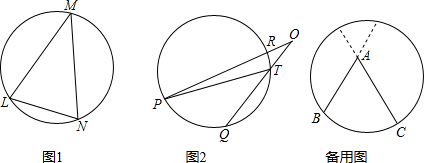
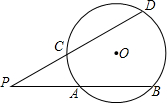 圆心角度数的一半.类似地,我们定义:顶点在圆外,并且两边都和圆相交的角叫做圆外角.
圆心角度数的一半.类似地,我们定义:顶点在圆外,并且两边都和圆相交的角叫做圆外角.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com