
题目列表(包括答案和解析)
(本题9分)如图,△ABC是直角三角形,∠ACB=90°.
(1)实践与操作 利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法).
①作△ABC的外接圆,圆心为O;
②以线段AC为一边,在AC的右侧作等边△ACD;
③连接BD,交⊙O于点F,连接AE,
(2)综合与运用 在你所作的图中,若AB=4,BC=2,则:
①AD与⊙O的位置关系是______.(2分)
②线段AE的长为__________.(2分)
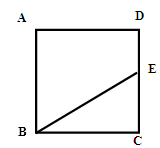
、(本题12分) 如图甲,在△ABC中,E是AC边上的一点,
(1)在图甲中,作出以BE为对角线的平行四边形BDEF,使D、F分别在BC和AB边上;
(2)改变点E的位置,则图甲中所作的平行四边形BDEF有没有可能为菱形?若有,请在图乙中作出点E的位置(用尺规作图,并保留作图痕迹);若没有,请说明理由.
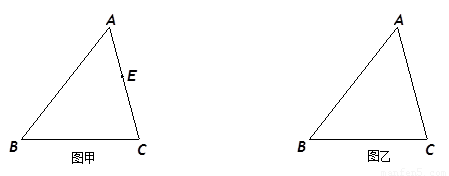 |
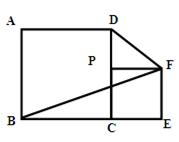
(本题10分)已知:正方形ABCD的边长为a,P是边CD上一个动点不与C、D重合,CP=b,以CP为一边在正方形ABCD外作正方形PCEF,连接BF、DF.
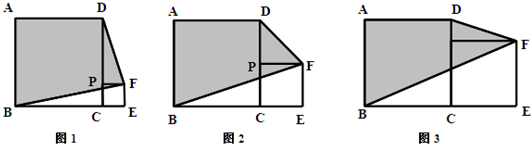
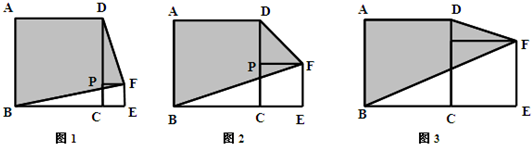
1.观察计算:(1)如图1,当a=4,b=1时,四边形ABFD的面积为 ;
(2)如图2,当a=4,b=2时,四边形ABFD的面积为 ;
(3)如图3,当a=4,b=3时,四边形ABFD的面积为 ;
2.探索发现:(4)根据上述计算的结果,你认为四边形ABFD的面积与正方形ABCD的面积之间有怎样的关系?证明你的结论;

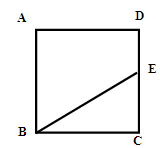
3.综合应用:(5)农民赵大伯有一块正方形的土地(如图),由于修路被占去一块三角形的地方△BCE,但决定在DE的右侧补给赵大伯一块土地,补偿后的土地为四边形ABMD,且四边形ABMD的面积与原来正方形土地的面积相等,M、E、B三点要在一条直线上,请你画图说明,如何确定M点的位置.(要求尺规作图,保留作图痕迹)
(本题9分)如图,△ABC是直角三角形,∠ACB=90°.
(1)实践与操作 利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法).
①作△ABC的外接圆,圆心为O;
②以线段AC为一边,在AC的右侧作等边△ACD;
③连接BD,交⊙O于点F,连接AE,
(2)综合与运用 在你所作的图中,若AB=4,BC=2,则:
①AD与⊙O的位置关系是______.(2分)
②线段AE的长为__________.(2分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com