(本题满分10分)如图，阳春三月里小黄同学在操场上放风筝，风筝从A处起飞，几分钟后便飞到C处，此时，在AQ的延长线上B处的小宋同学发现自己的位置与风筝和旗杆PQ的顶点P在同一直线上．

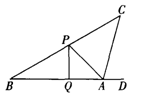
 1. (1)已知旗杆高10米，若在B处测得旗杆顶点P的仰角为30°，在A处测得点P的仰角为45°，试求A、B之间的距离．

 　2. (2)此时，在A处背向旗杆又测得风筝的仰角为75°，若将绳子在空中视为一条线段，求绳子的长度AC(结果保留根号)．

(本题满分10分)如图，阳春三月里小黄同学在操场上放风筝，风筝从A处起飞，几分钟后便飞到C处，此时，在AQ的延长线上B处的小宋同学发现自己的位置与风筝和旗杆PQ的顶点P在同一直线上．

 1. (1)已知旗杆高10米，若在B处测得旗杆顶点P的仰角为30°，在A处测得点P的仰角为45°，试求A、B之间的距离．

 　2. (2)此时，在A处背向旗杆又测得风筝的仰角为75°，若将绳子在空中视为一条线段，求绳子的长度AC(结果保留根号)．

（本小题满分10分）

如图，已知点E在直角△ABC的斜边AB上，以AE为直径的⊙O与直角边BC相切于点D，∠B = 30°．

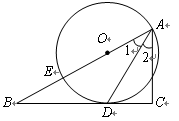
求证：1.（1）AD平分∠BAC，2.（2）若BD =  ，求B E的长．

（本小题满分10分）

    学习过三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化.

类似的，可以在等腰三角形中建立边角之间的联系，我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）.如图，在△ABC中，AB=AC，顶角A的正对记作sadA，这时sad A=.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.

根据上述对角的正对定义，解下列问题：

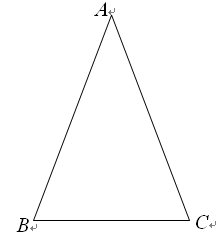
（1）sad 的值为（   ）A.       B.1  C.      D.2

（2）对于，∠A的正对值sad A的取值范围是        .

（3）已知，其中为锐角，试求sad的值.

（本小题满分10分）

数形结合作为一种数学思想方法，数形结合的应用大致又可分为两种情形：或者借助于数的精确性来阐明形的某些属性，即“以数解形”；或者借助形的几何直观性来阐明数之间的某种关系，即 “以形助数”。                                                            

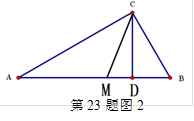如浙教版九上课本第109页作业题第2题：如图1，已知在△ABC中，∠ACB=900，CD⊥AB，D为垂足。易证得两个结论：(1)AC·BC = AB·CD   (2)AC2= AD·AB

（1）请你用数形结合的“以数解形”思想来解：如图2，已知在△ABC中（AC>BC），∠ACB=900，CD⊥AB，D为垂足， CM平分∠ACB,且BC、AC是方程x2-14x+48=0的两个根，求AD、MD的长。

（2）请你用数形结合的“以形助数”思想来解： 设a、b、c、d都是正数，满足a：b=c：d,且a最大。求证：a+d>b+c（提示：不访设AB=a,CD=d,AC=b,BC=c，构造图1）