（本题12分） 如图，抛物线y=ax²＋bx＋c交x轴于点A（－3，0），点B（1，0），交y轴于点E（0，－3）。点C是点A关于点B的对称点，点F是线段BC的中点，直线l过点F且与y轴平行。直线y=－x＋m过点C，交y轴于D点.

⑴求抛物线的函数表达式；

   ⑵点K为线段AB上一动点，过点K作x轴的垂线与直线CD交于点H，与抛物线交于     点G，求线段HG长度的最大值；

⑶在直线l上取点M，在抛物线上取点N，使以点A，C，M，N为顶点的四边形是平行四边形，求点N的坐标.

（本题12分）△ABC中，∠A=∠B=30°，AB=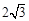．把△ABC放在平面直角坐标系中，使AB的中点位于坐标原点O (如图)，△ABC可以绕点O作任意角度的旋转．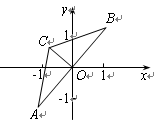

【小题1】(1)　当点B在第一象限，纵坐标是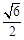时，求点B的横坐标；
【小题2】(2)　如果抛物线的对称轴经过点C，请你探究：
①当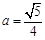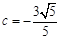，，时，A，B两点是否都在这条抛物线上？并说明理由；
②设，是否存在这样的m的值，使A，B两点不可能同时在这条抛物线上？若存在，直接写出m的值；若不存在，请说明理由．

（本题12分）某公司开发研制太阳能光伏电池.产品投产上市一年来，公司经历了由初期的亏损到后来逐步盈利的过程（公司对经营的盈亏情况每月最后一天结算1次）.公司累积获得的利润y（万元）与销售时间第x（月）之间的函数关系式（即前x个月的利润总和y与x之间的关系）对应的点都在如图所示的图象上.该图象从左至右，依次是线段OA、曲线AB和曲线BC，其中曲线AB为抛物线的一部分，点A为该抛物线的顶点，曲线BC为另一抛物线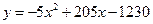的一部
分，且点A，B，C的横坐标分别为4，10，12.
（1）求该公司累积获得的利润y（万元）与时间第x（月）之间的函数关系式；
（2）直接写出第x个月所获得S（万元）与时间x（月）之间的函数关系式（不需要写出计算过程）；
（3）前12个月中，第几个月该公司所获得的利润最多？最多利润是多少万元？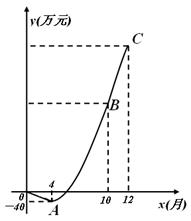

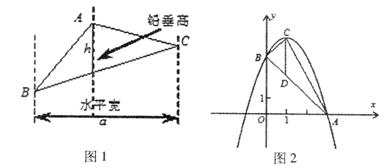
（本题12分）阅读材料：如图1，过△ABC的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”（a），中间的这条直线在△ABC内部的线段的长度叫△ABC的“铅垂高”（h）.我们可行出生种计算三角形面积的新方示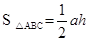：，即三角形面积等于水平宽与铅垂高乘积的一半.

解答下列问题:

如图2，抛物线顶点C（1，4），交x轴于点A（3，0），交y轴于点B.

（1）求抛物线和直线AB的解析式；

（2）求△ABC的铅垂高CD及S_△ABC

（3）设点P是抛物线（在第一象限内）上的一个动点，是否存在一点P，使，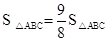

若存在，求出P点的坐标；若不存在，请说明理由.