练习册

  • 练习册
  • 试题
    [8分]已知:二次函数 求证:不论a取何值时,抛物线与x轴都有两个不同的交点. 【查看更多】

     

    题目列表(包括答案和解析)

    精英家教网已知关于x的一元二次方程x2-（m-1）x+m-3=0．
    （1）求证：不论m取何值时，方程总有两个不相等的实数根．
    （2）若直线y=（m-1）x+3与函数y=x2+m的图象C1的一个交点的横坐标为2，求关于x的一元二次方程x2-（m-1）x+m-3=0的解．
    （3）在（2）的条件下，将抛物线y=x2-（m-1）x+m-3绕原点旋转180°，得到图象C2，点P为x轴上的一个动点，过点P作x轴的垂线，分别与图象C1、C2交于M、N两点，当线段MN的长度最小时，求点P的坐标．

    查看答案和解析>>

    已知关于x的一元二次方程x2-（m-1）x+m-3=0．
    （1）求证：不论m取何值时，方程总有两个不相等的实数根．
    （2）若直线y=（m-1）x+3与函数y=x2+m的图象C1的一个交点的横坐标为2，求关于x的一元二次方程x2-（m-1）x+m-3=0的解．
    （3）在（2）的条件下，将抛物线y=x2-（m-1）x+m-3绕原点旋转180°，得到图象C2，点P为x轴上的一个动点，过点P作x轴的垂线，分别与图象C1、C2交于M、N两点，当线段MN的长度最小时，求点P的坐标．

    查看答案和解析>>

    （2010•石景山区二模）已知关于x的一元二次方程x2-（m-1）x+m-3=0．
    （1）求证：不论m取何值时，方程总有两个不相等的实数根．
    （2）若直线y=（m-1）x+3与函数y=x2+m的图象C1的一个交点的横坐标为2，求关于x的一元二次方程x2-（m-1）x+m-3=0的解．
    （3）在（2）的条件下，将抛物线y=x2-（m-1）x+m-3绕原点旋转180°，得到图象C2，点P为x轴上的一个动点，过点P作x轴的垂线，分别与图象C1、C2交于M、N两点，当线段MN的长度最小时，求点P的坐标．

    查看答案和解析>>

    已知：一元二次方程．

    (1)求证：不论k为何实数时，此方程总有两个实数根；

    (2)设k＜0，当二次函数的图象与x轴的两个交点A、B间的距离为4时，求此二次函数的解析式；

    (3)在(2)的条件下，若抛物线的顶点为C，过y轴上一点M(0，m)作y轴的垂线l，当m为何值时，直线l与△ABC的外接圆有公共点？

    如图，在△ABC中，∠B＝45°，BC＝5，高AD＝4，矩形EFPQ的一边QP在BC边上，E、F分别在AB、AC上，AD交EF于点H．

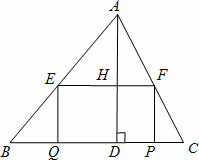
    (1)求证：；

    (2)设EF＝x，当x为何值时，矩形EFPQ的面积最大？并求出最大面积；

    (3)当矩形EFPQ的面积最大时，该矩形EFPQ以每秒1个单位的速度沿射线DA匀速向上运动(当矩形的边PQ到达A点时停止运动)，设运动时间为t秒，矩形EFPQ与△ABC重叠部分的面积为S，求S与t的函数关系式，并写出t的取值范围．

    查看答案和解析>>

    已知关于x的一元二次方程数学公式．
    （1）求证：无论m取任何实数，方程都有两个实数根；
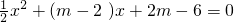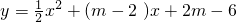    （2）当m＜3时，关于x的二次函数数学公式的图象与x轴交于A、B 两点（点A在点B的左侧），与y轴交于点C，且2AB=3OC，求m的值；
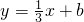    （3）在（2）的条件下，过点C作直线l∥x轴，将二次函数图象在y轴左侧的部分沿直线l翻折，二次函数图象的其余部分保持不变，得到一个新的图象，记为G．请你结合图象回答：当直线数学公式与图象G只有一个公共点时，b的取值范围．

    查看答案和解析>>


    同步练习册答案