练习册

  • 练习册
  • 试题
    多边形(多边形的性质及其正多边形的特征) 例3.(1)正方形具有而菱形不一定具有的性质( ) A.四边都相等 B.对角线互相垂直且平分 C.对角线相等 D.对角线平分一组对角 (2)下列命题中假命题的是( ) A.对角线互相平分的四边形是平行四边形. B.两条对角线相等的四边形是矩形. C.两条对角线互相垂直的矩形是正方形 D.两条对角线相等的菱形是正方形 (3)检查一个门框是矩形的方法是( ) A.测量两条对角线是否相等 B.测量有三个角是直角 C.测量两条对角线是否互相平分 D.测量两条对角线是否互相垂直 (4)顺次连接矩形各边中点所得的四边形是( ) A.矩形 B.菱形 C.梯形 D.正方形 (5)菱形的周长等于高的8倍.则其最大内角等于( ) A.60° B.90° C.120° D.150° (6)矩形ABCD中.AB=8.BC=6.E.F是AC的三等分点.则△BEF的面积是( ) A.8 B.12 C.16 D.24 Ⅱ.中考演练 【查看更多】

     

    题目列表(包括答案和解析)

    古人曾研究过所谓的“多边形数”：即能用点排成多边形（通常排成正多边形）的阵列表示的数．在数学史上曾一度为不少专业和业余的数学家所青睐，人们认为这些奇妙的数一定有它特殊的性质，因为她们的确很具数学美．下图所示是前5个三角形数．第1个三角形数是1，第2个三角形数是3，第3个三角形数是6…，依此规律回答以下三个问题：
    （1）第6个三角形数是
    21
    21
    ；
    （2）第n个三角形数是
    n(n+1)
    2
    n(n+1)
    2
    （用含n的式子表示，其中n表示正整数）；
    （3）第2013个三角形数与2011个三角形数的差是
    4025
    4025
    ．

    查看答案和解析>>

    古人曾研究过所谓的“多边形数”：即能用点排成多边形（通常排成正多边形）的阵列表示的数．在数学史上曾一度为不少专业和业余的数学家所青睐，人们认为这些奇妙的数一定有它特殊的性质，因为她们的确很具数学美．下图所示是前5个三角形数．第1个三角形数是1，第2个三角形数是3，第3个三角形数是6…，依此规律回答以下三个问题：
    （1）第6个三角形数是________；
    （2）第n个三角形数是________（用含n的式子表示，其中n表示正整数）；
    （3）第2013个三角形数与2011个三角形数的差是________．

    查看答案和解析>>

    相似多边形的两个基本性质是（    ），（    ）。

    查看答案和解析>>

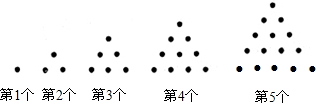
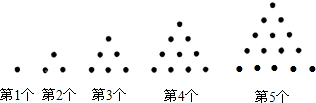
    几个同学在讨论数学问题时作了如下发言：甲说，因为三角形中最多只有一个钝角，由邻补角的性质知，三角形的外角中最多只有一个锐角；乙说，在求n条边都相等的n边形的内角度数时，可用结论“内角度数等于(180°－·360°)”；丙说，多边形的内角和总比外角和大；丁说，n边形的边数每增加一条，对角线就增加n条．其中说法正确的同学是

    [　　]

    A．甲、丙

    B．乙、丁

    C．甲、丁

    D．以上都不对

    查看答案和解析>>

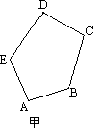
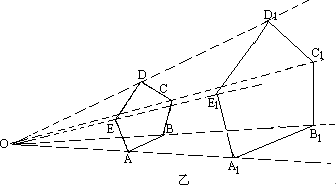
    利用位似图形的性质，把图所示甲中的多边形ABDE放大2倍

    查看答案和解析>>


    同步练习册答案