
题目列表(包括答案和解析)
(10分)如图,已知抛物线与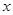 轴交于A(1,0),B(
轴交于A(1,0),B(![]() ,0)两点,与
,0)两点,与![]() 轴交于点
轴交于点
C(0,3),抛物线的顶点为P,连结AC.
(1)求此抛物线的解析式;
(2)在抛物线上找一点D,使得DC与AC垂直,且直线DC与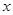 轴交于点Q,求点D的坐标;
轴交于点Q,求点D的坐标;
(3)抛物线对称轴上是否存在一点M,使得S△MAP=2S△ACP,若存在,求出M点坐标;若不存在,请说明理由.
(本题满分10分)
⑴如图,已知∠AOB=90º,∠BOC=30º,OM平分∠AOB,ON平分∠BOC,求∠MON的度数;
⑵如果⑴中∠AOB=α,∠BOC=β(β为锐角),其他条件不变,求∠MON的度数;
⑴ 从⑴、⑵的结果中能得出什么结论?

(本题满分10分)如图,已知一矩形ABCD,若把△ABE沿折痕BE向上翻折,A点恰好落在DC上,设此点为F,且这时AE:ED=5:3,BE=5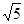 ,这个矩形的长宽各是多少?
,这个矩形的长宽各是多少?

(本题10分)如图,已知在⊙O中,直径AB为8cm,弦AC为4 cm,∠ACB的平分线交⊙O于D,连结BC,AD.【小题1】(1)求BC的长. 【小题2】(2)求∠CAD的度数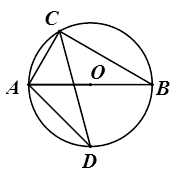
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com