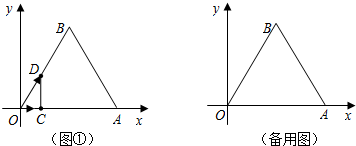(本题满分12分,任选一题作答.)
Ⅰ、如图①,在平面直角坐标系中,O为坐标原点,边长为5的正三角形OAB的OA边在x轴的正半轴上.点C、D同时从点O出发,点C以1单位长/秒的速度向点A运动,点D以2个单位长/秒的速度沿折线OBA运动.设运动时间为t秒,0<t<5.

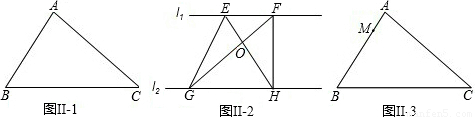
(1)当
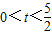
时,证明DC⊥OA;
(2)若△OCD的面积为S,求S与t的函数关系式;
(3)以点C为中心,将CD所在的直线顺时针旋转60°交AB边于点E,若以O、C、E、D为顶点的四边形是梯形,求点E的坐标.
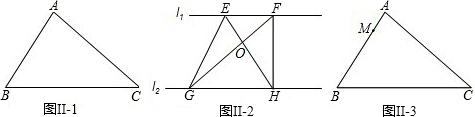
Ⅱ、(1)如图Ⅱ-1,已知△ABC,过点A画一条平分三角形面积的直线;
(2)如图Ⅱ-2,已知l
1∥l
2,点E,F在l
1上,点G,H在l
2上,试说明△EGO与△FHO面积相等.
(3)如图Ⅱ-3,点M在△ABC的边上,过点M画一条平分三角形面积的直线.


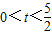 时,证明DC⊥OA;
时,证明DC⊥OA;