
题目列表(包括答案和解析)
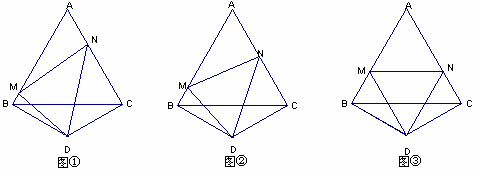
操作:如图①,△ABC是正三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角,角的两边分别交AB、AC边于M、N两点,连接MN.
探究:线段BM、MN、NC之间的关系,并加以证明.![]()
说明:⑴如果你经历反复探索,没有找到解决问题的方法,请你把探索过程中的某种思路写出来(要求至少写3步);⑵在你经历说明⑴的过程之后,可以从下列①、②中选取一个补充或更换已知条件,完成你的证明.
注意:选取①完成证明得10分;选取②完成证明得5分.
①![]() (如图②); ②
(如图②); ②![]() (如图③).
(如图③).
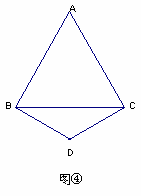
附加题:若点M、N分别是射线AB、CA上的点,其它条件不变,再探线段BM、MN、NC之间的关系,在图④中画出图形,并说明理由.
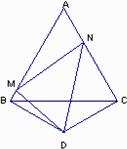
操作:如图,△ABC是正三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角,角的两边分别交AB、AC边于M、N两点,连接MN.
探究:线段BM、MN、NC之间的关系,并加以证明.
说明:(1)如果你经历反复探索,没有找到解决问题的方法,请你把探索过程中的某种思路写出来(要求至少写3步);
(2)在你经历说明(1)的过程之后,可以从下列①、②中选取一个补充或更换已知条件,完成你的证明.
注意:选取①完成证明得10分;选取②完成证明得5分.
①AN=NC(如图);
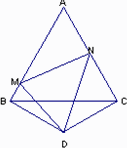
②DM∥AC(如图).
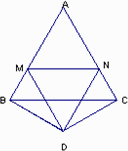
若点M、N分别是射线AB、CA上的点,其它条件不变,再探线段BM、MN、NC之间的关系,在图中画出图形,并说明理由.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com