
题目列表(包括答案和解析)
(本题满分10分,其中第(1)小题6分,第(2)小题4分)
如图,已知在△ABC中,点D在边AC上,CD∶AD=1∶2,![]() ,
,![]() .
.
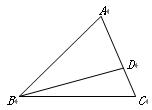
1.(1)试用向量![]() 表示向量
表示向量![]() ;
;
2.(2)求作:![]() .(不要求写作法,但要指出所作
.(不要求写作法,但要指出所作
图中表示结论的向量)
(本题满分10分,其中第(1)小题6分,第(2)小题4分)
如图,已知在△ABC中,点D在边AC上,CD∶AD=1∶2, ,
, .
.
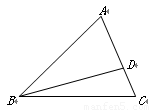
1.(1)试用向量 表示向量
表示向量 ;
;
2.(2)求作: .(不要求写作法,但要指出所作
.(不要求写作法,但要指出所作
图中表示结论的向量)
(本小题满分10分)
学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
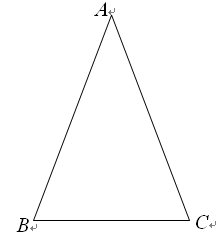
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A= .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述对角的正对定义,解下列问题:
(1)sad ![]() 的值为( )A.
的值为( )A. ![]() B.1 C.
B.1 C. ![]() D.2
D.2
(2)对于![]() ,∠A的正对值sad A的取值范围是 .
,∠A的正对值sad A的取值范围是 .
(3)已知![]() ,其中
,其中![]() 为锐角,试求sad
为锐角,试求sad 的值.
的值.
 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
 的值为( )
的值为( )A. | B.1 | C.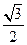 | D.2 |
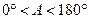 ,∠A的正对值sad A的取值范围是 .
,∠A的正对值sad A的取值范围是 .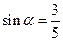 ,其中
,其中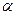 为锐角,试求sad
为锐角,试求sad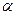 的值.
的值.(本小题满分10分)
学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=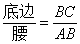 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述对角的正对定义,解下列问题:

(1)sad 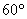 的值为( )A.
的值为( )A. 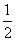 B.
1 C.
B.
1 C. 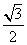 D.
2
D.
2
(2)对于 ,∠A的正对值sad A的取值范围是
.
,∠A的正对值sad A的取值范围是
.
(3)已知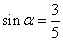 ,其中
,其中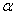 为锐角,试求sad
为锐角,试求sad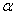 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com